Determination of Decisive Load Case Combinations with Superposition of Normal Stresses in Cross Section Points#
Introduction#
This document provides some explanations of examples for superposition of normal stresses in a cross section in order to receive the decisive load case combinations.
Theoretical Background#
In the lecture by Prof. Dr.-Ing. Bockhold and Mr. Vossen for the conference ‘Baustatik - Baupraxis 14, Universität Stuttgart’, the topic of the determination load case combinations for the design is discussed. A main focus is the possibility of the superposition of stresses in certain cross section points, as offered by SOFiSTiK with the program MAXIMA. In the following, the three examples of the lecture are presented and explained with the possibilities of SOFiSTiK.
Literature:
Prof. Dr.-Ing. Jörg Bockhold, Thomas Vossen: Einfluss einer computergestützten Schnittgrößenüberlagerung auf die Standsicherheit im Stahl- und Betonbau, Universität Stuttgart, Baustatik - Baupraxis 14, 2020, https://dx.doi.org/10.18419/opus-10762, ISBN: 978-3-00-064639-3
PDF of the lecture is included in the attachment.
Objectives#
Generate the system inclusive the design code, materials, cross sections
Generate the actions with the task Action Manager or with the program SOFiLOAD
Generate loads with the program SOFiLOAD
Run linear analysis
Generate action combinations in program MAXIMA (or in SSD task ‘Combinations’)
Generate superpositions for normal stress in beam elements using stress points of the corresponding cross section (or SSD task ‘Superpositions’)
Generate decisive load case combinations using SSD task ‘Combine Loads’ or task ‘Combine Results’ with button Automatic
First Example Chapter 2.1#
File: bb14-bockhold-vossen_example1.dat
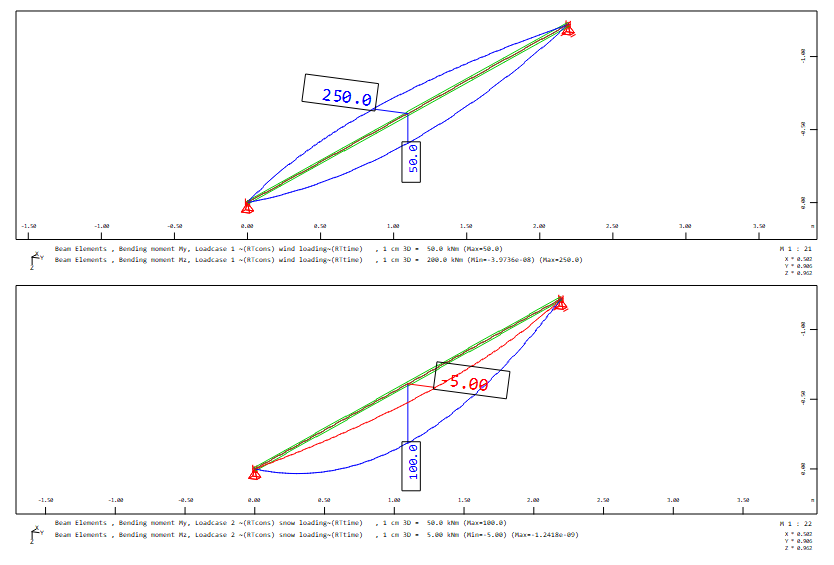
This is a numerical example which is input by a single-span girder with a rectangular cross-section and equivalent loads for the bending moment.
Load case |
Action |
Safety factor |
Combination coefficient |
|---|---|---|---|
1 |
Wind |
1.5 |
0.7 |
2 |
Snow |
1.5 |
0.7 |
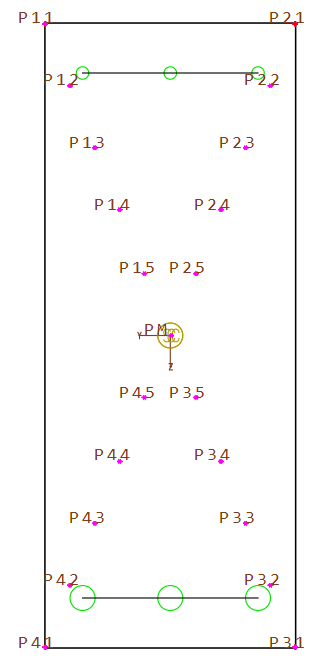
A rectangluar cross section is defined with additional stress points in the corners and inside.
As decribed in the lecture, a superposition of only the bending moments does here not lead to a goal. That is why a superposition of the normal forces in the stress points of the cross section is done.
+prog maxima
head
echo load,fact
comb 1 desi
act W
act S
supp 1 mami beam my,mz from 5 x 1[-] opt S lc 2101
supp 1 mami beam sig sele P11 from 5 x 1[-] opt S lc 2110
supp 1 mami beam sig sele P12 from 5 x 1[-] opt S lc 2112
supp 1 mami beam sig sele P13 from 5 x 1[-] opt S lc 2114
supp 1 mami beam sig sele P14 from 5 x 1[-] opt S lc 2116
supp 1 mami beam sig sele P15 from 5 x 1[-] opt S lc 2118
supp 1 mami beam sig sele P21 from 5 x 1[-] opt S lc 2120
supp 1 mami beam sig sele P22 from 5 x 1[-] opt S lc 2122
supp 1 mami beam sig sele P23 from 5 x 1[-] opt S lc 2124
supp 1 mami beam sig sele P24 from 5 x 1[-] opt S lc 2126
supp 1 mami beam sig sele P25 from 5 x 1[-] opt S lc 2128
supp 1 mami beam sig sele P31 from 5 x 1[-] opt S lc 2130
supp 1 mami beam sig sele P32 from 5 x 1[-] opt S lc 2132
supp 1 mami beam sig sele P33 from 5 x 1[-] opt S lc 2134
supp 1 mami beam sig sele P34 from 5 x 1[-] opt S lc 2136
supp 1 mami beam sig sele P35 from 5 x 1[-] opt S lc 2138
supp 1 mami beam sig sele P41 from 5 x 1[-] opt S lc 2140
supp 1 mami beam sig sele P42 from 5 x 1[-] opt S lc 2142
supp 1 mami beam sig sele P43 from 5 x 1[-] opt S lc 2144
supp 1 mami beam sig sele P44 from 5 x 1[-] opt S lc 2146
supp 1 mami beam sig sele P45 from 5 x 1[-] opt S lc 2148
end
With the superposition only for the maximum and minimum of the bending moments My and Mz the decisive load case combination for the design is not determined. As described in the lecture the decisive load case combination LFK 1002a is determined with the stress superposition in following stress points:
for minimum normal stress in point P11

for maximum normal stress in point P31

With MAXIMA it is also possible to determine the resultant of the vector using moment vectors My and Mz. An objective function which decribes the square root has to be input for the superposition type:
!*!Label Resultant of the vector
+prog maxima
head
echo load,fact
comb 11 desi
act W
act S
supp 11 max beam type 'sqr(my**2+mz**2)' from 5 x 1[-] opt S lc 3101
TXE LFK 1002a: SQR(180²+369.75²)=411.24 kNm
end
Second Example Chapter 2.2#
File: bb14-bockhold-vossen_example2.dat
A cantilevered steel beam HEA 220 is considered with a horizontal wind and snow loading.
Load case |
Action |
Safety factor |
Combination coefficient |
|---|---|---|---|
1 |
Wind |
1.5 |
0.6 |
2 |
Snow |
1.5 |
0.5 |
There are a bending moment Mzk = 25 kNm due to wind and a bending moment Myk = 25 kNm due to snow at the clamping point.
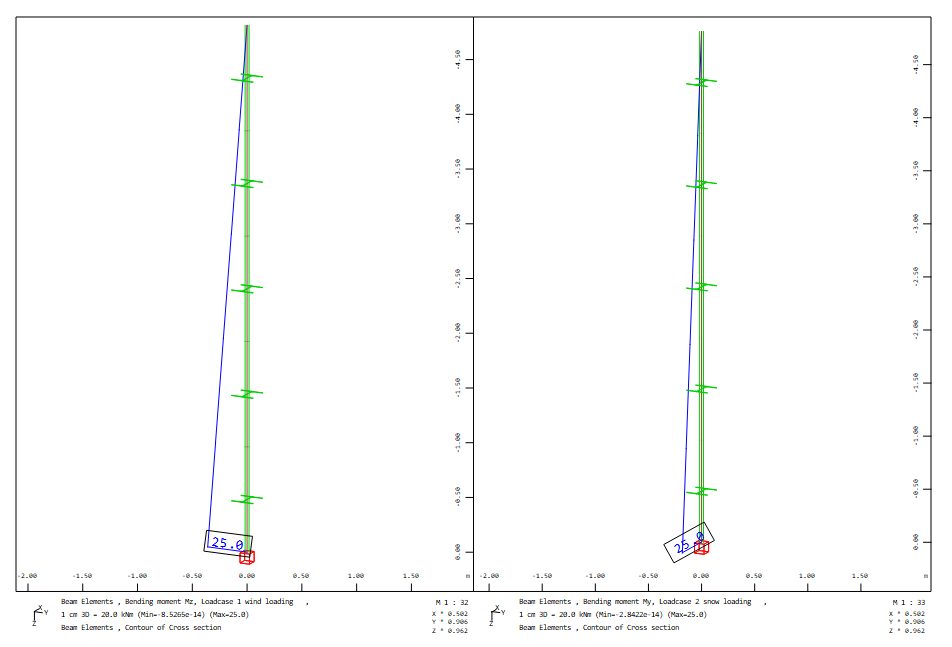
Here only superposition of the bending moments does not lead to the goal too. The decisive load combination can be detemined with a superposition of normal stresses in the default stress points of the cross section HEA 220. It is not necessary to input these default stress points in AQUA at the cross section. They are stored automatically and can be used in MAXIMA.
- Due to the stress distribution of the load cases 1 and 2 in the cross section following default stress points are examined:
in the middle of the upper flange Z- and lower flange Z-
in the four corners Y+Z+, Y-Z+, Y+Z- and Y-Z-
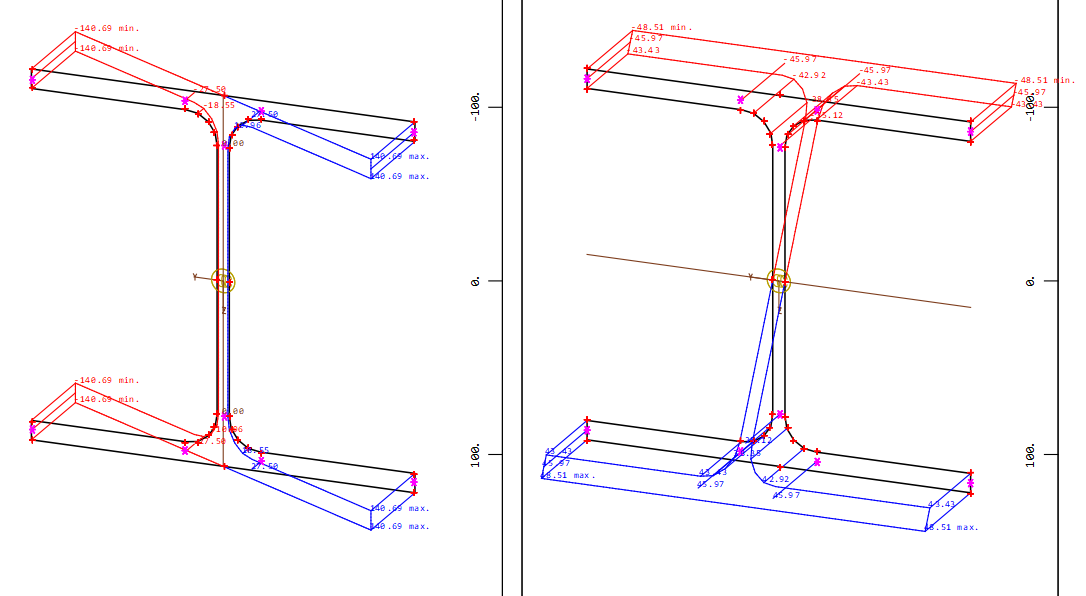
As can be seen in the stress distributions of the load cases 1 and 2 the decisive load case combination LFK 1002 is determined:
for point Y-Z+ max-sig

or for point Y+Z- min-sig

The load case combination LFK 1001 in the lecture is not determined, because the action S with LC 2 does not become a leading action due to the stress distribution and the factors.
Determination of the Sums for Cross Section Point Y-Z+
Load case |
Leading action |
Accompanying action |
Difference |
Result |
|---|---|---|---|---|
1 (wind) |
1.5*140.69=211.035 MPa |
1.5*0.6*140.69=126.621 MPa |
84.414 MPa |
leading action |
2 (snow) |
1.5*48.51=72.765 MPa |
1.5*0.5*48.51=36.3825 MPa |
36.3825 MPa |
accompanying action |
It is also possible to use the SSD tasks ‘Define Combiantions’ and ‘Superpositioning’ instead of MAXIMA with a TEDDY input
Steel structures are often calculated according to second order theory. Since the superposition principle does not apply here, the loads are combined SOFiSTiK offers the possibility to automatically determine the load case combinations in the SSD with the task ‘Combine Loads’ without using MAXIMA directly
File: ssd2022_bb14-bockhold-vossen_example2.sofistik
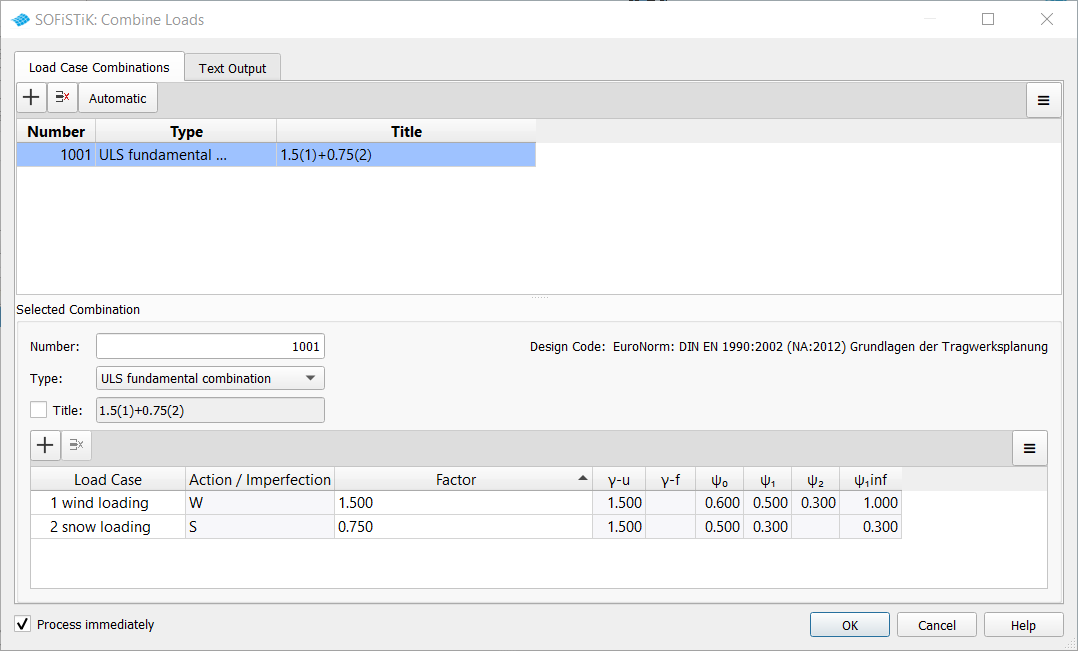
Using the button Automatic a subdialog is opened.
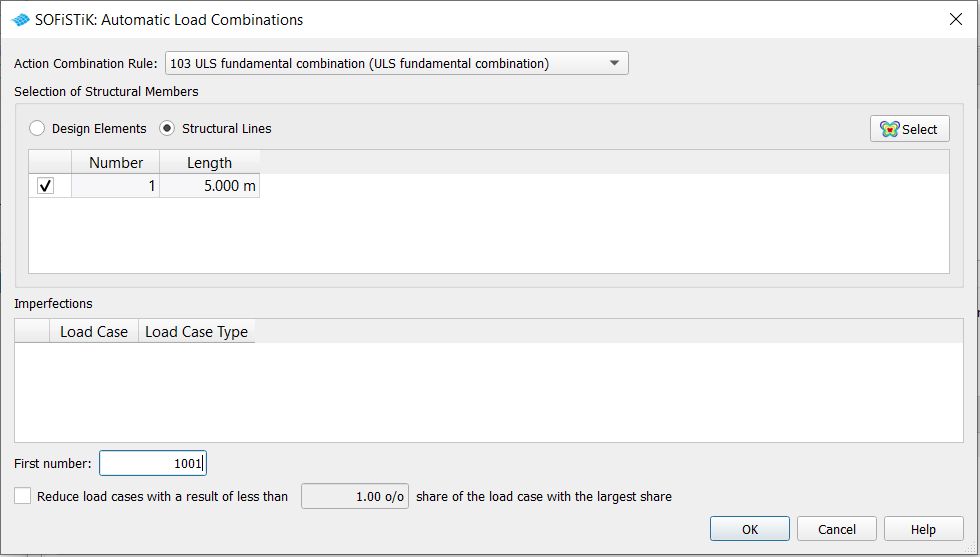
Internally MAXIMA is running similar as described with the DAT file. The determined load case combinations are displayed as a result. These load case combinations are then converted into a load input for SOFiLOAD and can be calculated according to second order theory with the task ‘Analysis of Combined Loads’. For this example the decisive load case combination is: 1.5 * LC 1(W) + 0.75 * LC 2(S)
Third Example Chapter 3#
File: bb14-bockhold-vossen_example3.dat
The third example is a rectangular cross section with following loading:
tension normal force Nk = 800 kN in load case 1 action W wind
bending moment Myk in load case 2 action S snow
Load case |
Action |
Safety factor |
Combination coefficient |
|---|---|---|---|
1 |
Wind |
1.5 |
0.7 |
2 |
Snow |
1.5 |
0.7 |
A rectangluar cross section is defined with additional stress points in the corners and inside.
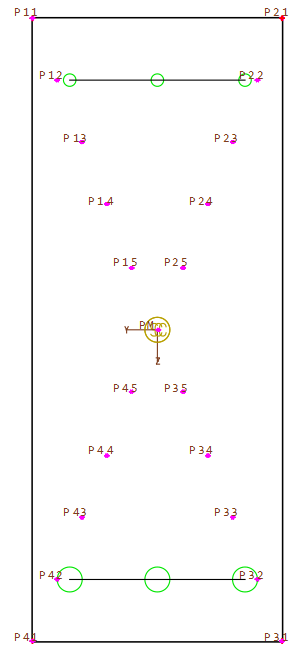
The MAXIMA input is similar to the first example. Due to uniaxial bending in LC 2 it is not necessary to calculated all defined stress points.
+prog maxima
head
echo load,fact
comb 1 desi
act W
act S
supp 1 mami beam my,n from 5 x 1[-] opt S lc 2101
supp 1 mami beam sig sele P11 from 5 x 1[-] opt S lc 2110
supp 1 mami beam sig sele P12 from 5 x 1[-] opt S lc 2112
supp 1 mami beam sig sele P13 from 5 x 1[-] opt S lc 2114
supp 1 mami beam sig sele P14 from 5 x 1[-] opt S lc 2116
supp 1 mami beam sig sele P15 from 5 x 1[-] opt S lc 2118
$supp 1 mami beam sig sele P21 from 5 x 1[-] opt S lc 2120 ! = P11 - P15 uniaxial bending
$supp 1 mami beam sig sele P22 from 5 x 1[-] opt S lc 2122
$supp 1 mami beam sig sele P23 from 5 x 1[-] opt S lc 2124
$supp 1 mami beam sig sele P24 from 5 x 1[-] opt S lc 2126
$supp 1 mami beam sig sele P25 from 5 x 1[-] opt S lc 2128
supp 1 mami beam sig sele P31 from 5 x 1[-] opt S lc 2130 ! LFK 2 = LF 3130 max-sig
supp 1 mami beam sig sele P32 from 5 x 1[-] opt S lc 2132
supp 1 mami beam sig sele P33 from 5 x 1[-] opt S lc 2134 ! LFK 1 = LF 3134 max-sig
supp 1 mami beam sig sele P34 from 5 x 1[-] opt S lc 2136
supp 1 mami beam sig sele P35 from 5 x 1[-] opt S lc 2138
$supp 1 mami beam sig sele P41 from 5 x 1[-] opt S lc 2140 ! = P31 - 35 uniaxial bending
$supp 1 mami beam sig sele P42 from 5 x 1[-] opt S lc 2142
$supp 1 mami beam sig sele P43 from 5 x 1[-] opt S lc 2144
$supp 1 mami beam sig sele P44 from 5 x 1[-] opt S lc 2146
$supp 1 mami beam sig sele P45 from 5 x 1[-] opt S lc 2148
The superposition of the normal stress in the defined stress points shows here a peculiarity. The load case combination LFK 1 which is decribed in the lecture is not determined at the corners of the cross section rather in inner stress points.
The decisive stress point is P33:
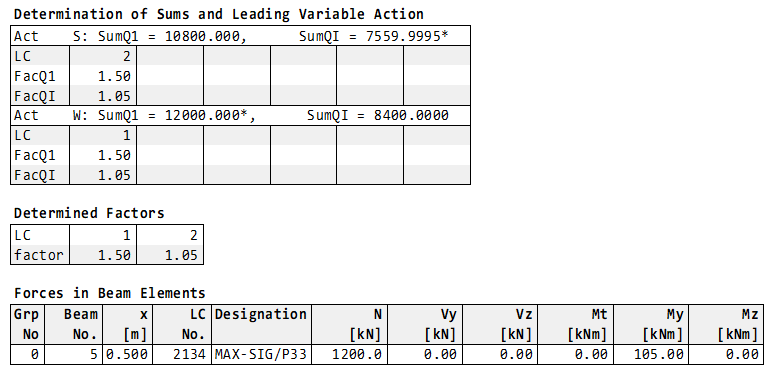
The load case combination LFK 2 is calculated in stress point P31 (corner) by MAXIMA:
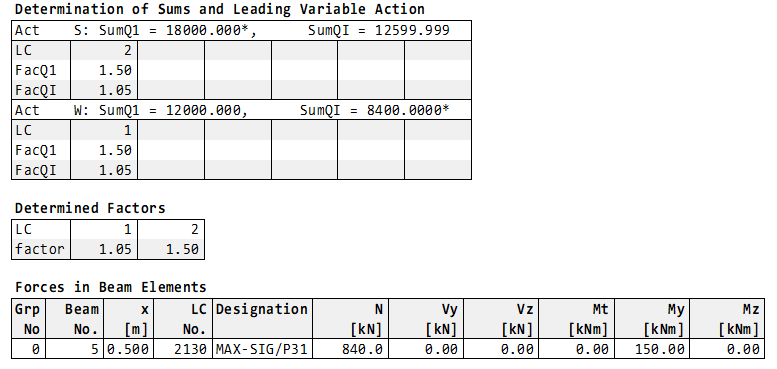
This example clearly shows that the stresses within the cross section are also superimposed.
In order to avoid the input effort with AQUA and MAXIMA, the use of the SSD tasks ‘Combine Loads’ or ‘Combine Results’ is recommended here with the automatic detemination of the load case combinations.
File: ssd2022_bb14-bockhold-vossen_example3.sofistik
The workflow in the task ‘Combine loads’ is described for example 2. The task ‘Combine Results’ works similar, however, the results of the initial load cases are combined here via load case combinations.
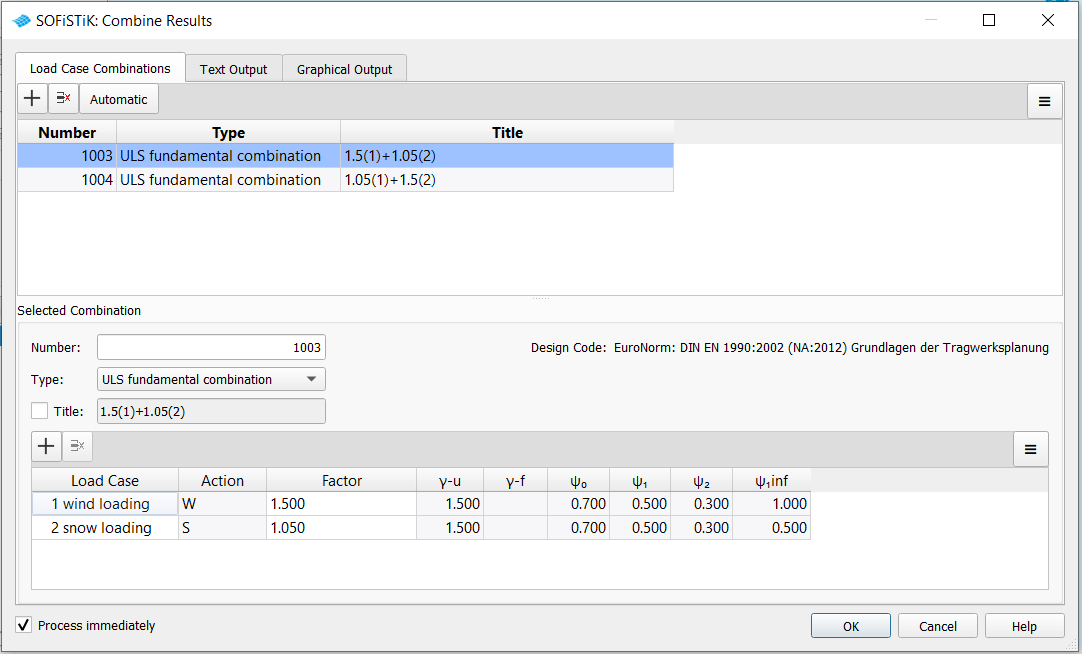
With the button Automatic and using the default target functions, the by an internal MAXIMA run determined load case combinations are:
for LFK1 1.5 * LC 1 (W) + 1.05 * LC 2 (S)
for LFK2 1.05 * LC 1 (W) + 1.5 * LC 2 (S)
Remarks#
The lecture by Prof. Dr.-Ing. Bockhold and Mr. Vossen shows very well that it is necessary to critically examine automatically determined superposition results.
SOFiSTiK offers several options for the superposition using action combinations. The described workflow of the automatically determination of load case combinations with the SSD tasks ‘Combine Loads’ and ‘Combine Results’ is also implemented in the program COLUMN (design of columns).