Storeys and Towers Concept

Storey Concept

For the assessment of structural seismic response, storey-based design criteria are an important ingredient in an engineer’s toolbox. The following figure shows a multi-storey building and corresponding storey definitions.

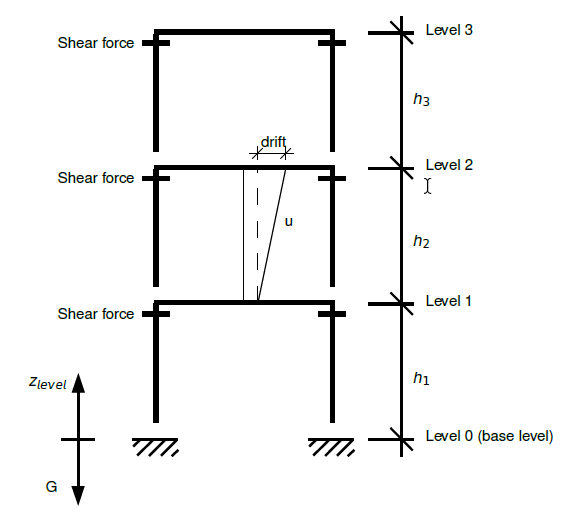
Definition of storeys in a multi-storey building

The \(z_{level}\) axis has its origin at the global coordinate system origin and always points upwards, opposed to gravity.

Each storey is characterised by a specific elevation which is defined in reference to the \(z_{level}\) axis. At this elevation a horizontal plane is implied, which - by definition - marks the top of the storey. In vertical direction, the storey extends from its (top) elevation down to the top elevation of the storey below. As a result, the storey height is determined by the vertical distance between these two elevations.

The storey level with the lowest elevation constitutes the base storey.

Note

By definition, the storey height of the base storey is always \(h = 0\).

The actual association of finite element nodes with storeys is based on their respective z-positions. While the initial ‘search boxes’ in lateral directions for this precedure are infinite, as a result of this topological analysis, each storey will be assigned bounding lateral extensions in global X- and Y-directions, derived from the extremal positioned associated nodes.

Note

A restriction of the ‘search boxes’ in lateral directions can be accomplished using Towers.

Tower Concept

Skyscrapers featuring more than one tower or split level scenarii require special attention when assessing seismic performance. To perform a qualified and efficient seismic assessment based on storey criteria, grouping of storeys into independent entities - we call these Towers - is a prerequisite.

Towers are an extension to the storey concept. A tower is characterised by the elevation of its base \(z_{base}\) and optional lateral limits described by the contour of a 4-point polygon. With such a tower, storeys with \(z_{level} >= z_{base}\) may be associated. The vertical extension of a tower is hence implied by the largest \(z_{level}\) of an associated storey.

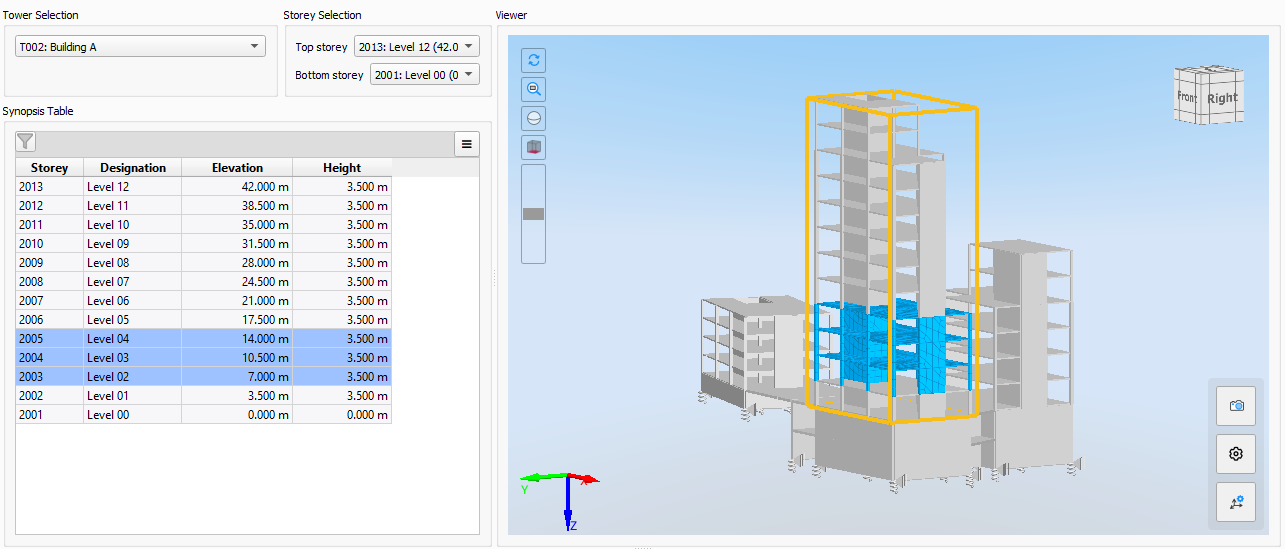
View of a tower and associated storeys in a multi-tower building

Note

At each tower base, a corresponding base storey object with height \(h = 0\) is generated.

For such a model, the actual association of finite element nodes with storeys, the same topological procedure takes place as described above. This time however, the ‘search boxes’ in lateral directions are defined by the respective lateral limits of the towers (4-point polygon contour).

Note

Storeys being associated with different towers are regarded as (mechanically) independent; even if they are located at the same elevations. Assessment of structural response, e.g., computation of storey drifts and storey checking, is undertaken per tower.