Double T-Beam Post Tensioned Concrete Bridge#
Introduction#
This tutorial deals with a simple 2-span post tensioned concrete double T-beam bridge. The analytical model of the bridge consists of beam elements and a slab to connect the two T-beams. The piers are modelled with beam elements as well.
Note
A basic SOFiSTiK knowledge is required for this tutorial. The standard workflow is explained inside the General Workflow description. Inside this tutorial we show only the project specific workflows, which are different from the basic workflow.
Objectives#
The main objective in this tutorial is to show the workflow using a “hybrid” model, with beams and slabs for the bridge deck. The system generation will be done inside SOFiPLUS. All the other objectives from starting a project up to performing analysis and design are the same as described in the standard workflow. Here we will focus on the settings necessary for a “hybrid” bridge system.
Project Description#
The idea of this tutorial is to guide you through a simple DTB (Double-T-Beam) post tensioned concrete bridge project, showing the important program tools and functions for this type of bridge.
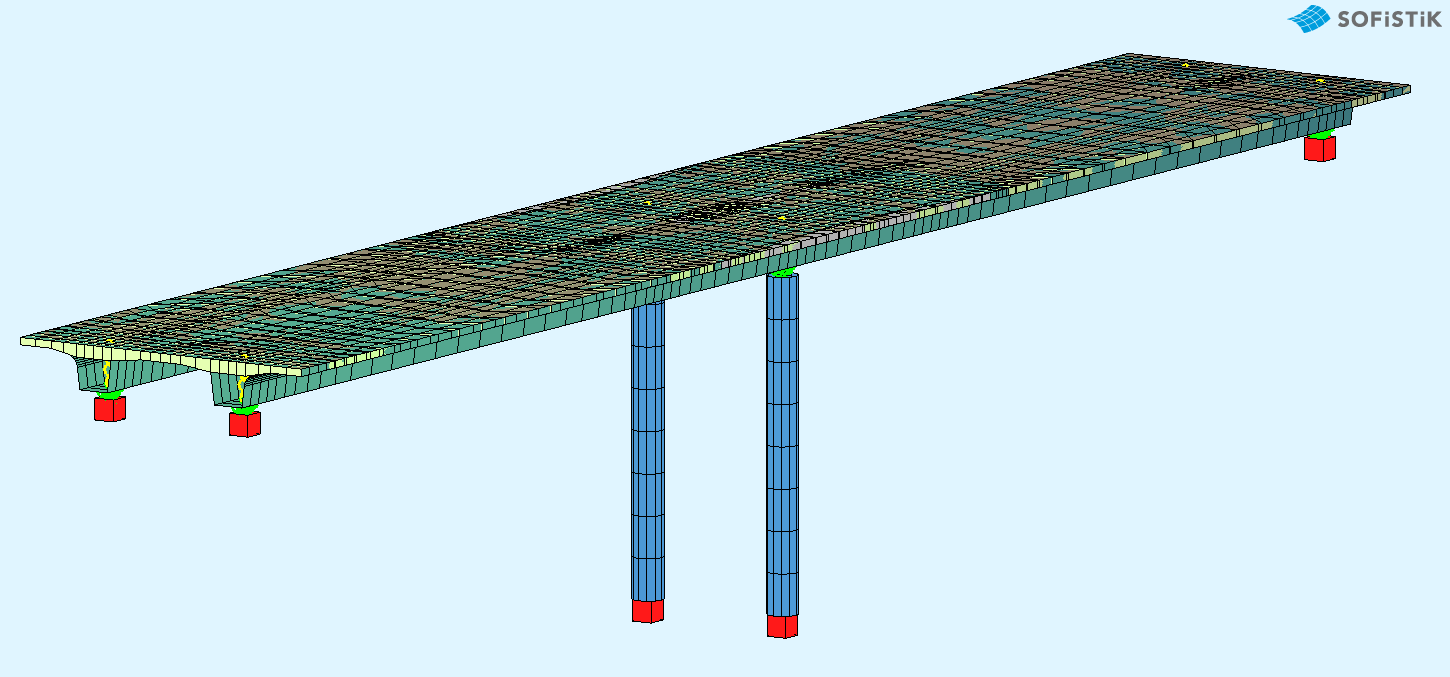
Bridge Axis:#
The following table shows the main spans and stations for the axis definition.
Spans [m] |
1.00 |
32.5 |
32.5 |
1.0 |
|||||
Stations [m] |
10.0 |
11.0 |
43.5 |
76.0 |
77.0 |
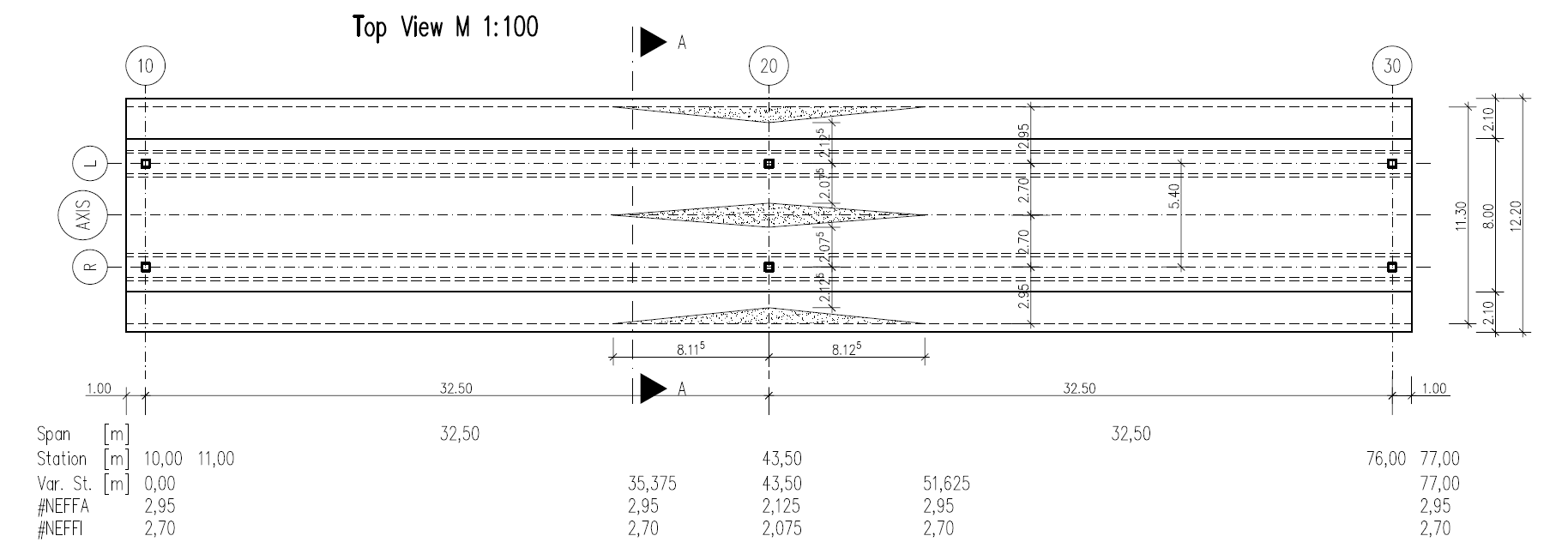
Along the bridge axis we will use a variable for the non-effective parts of the cross sections. Please see the following table with the necessary input values.
Station [m] |
0.000 |
35.375 |
43.500 |
51.625 |
90.000 |
#NEFFO [m] |
2.950 |
2.950 |
2.125 |
2.950 |
2.950 |
#NEFFI [m] |
2.700 |
2.700 |
2.075 |
2.700 |
2.700 |
Bridge Materials:#
The following table shows the necessary materials. As you can see, we are using different material numbers for bridge deck and column, although the concrete material is the same. This is a common setting inside SOFiSTIK to be able to split up the results for a better overview.
Number |
Title |
Strength |
|---|---|---|
1 |
Concrete pier |
C 30/37 |
2 |
Reinforcement pier |
B 500B |
11 |
Concrete T-beam |
C 40/50 |
12 |
Reinforcement T-beam |
B 500B |
13 |
Reinforcement T-beam stirrups |
B 500B |
14 |
Prestressing steel T-beam |
Y 1770 |
21 |
Concrete bridge deck |
C 40/50; \(\gamma\) = 0 kN/m³ |
22 |
Reinforcement bridge deck |
B 500B |
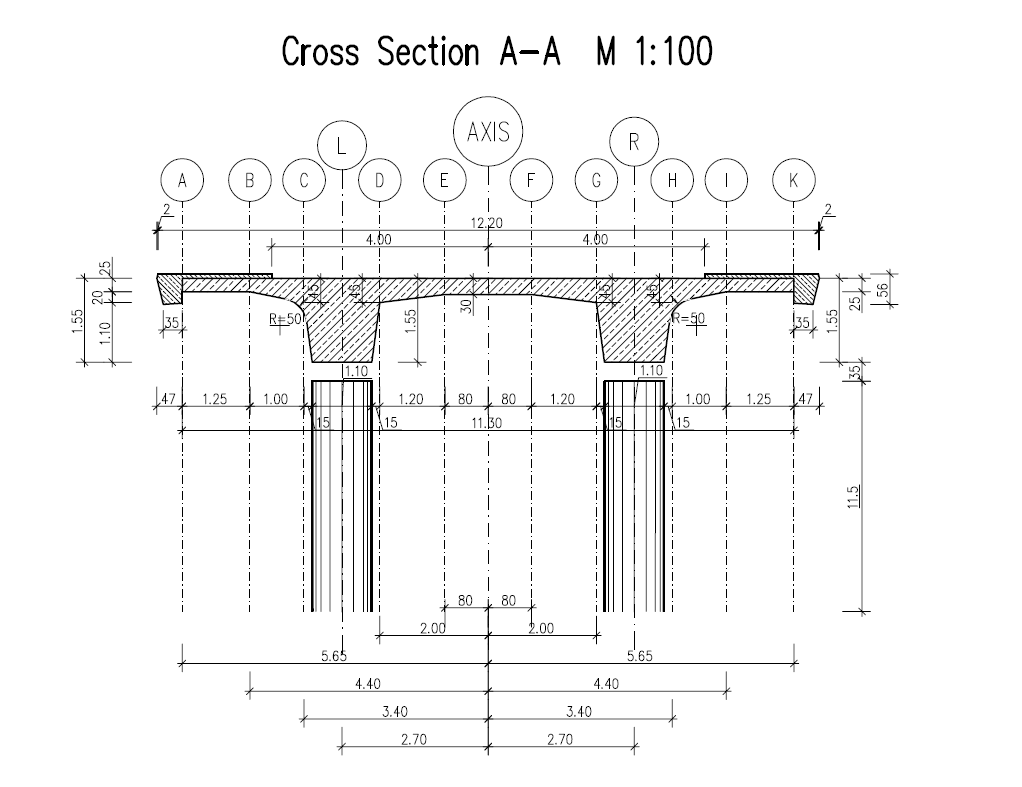
Cross sections#
Number |
Title |
Dimensions |
|---|---|---|
1 |
Pier |
D = 1.100 m |
Construction stages#
Stage Number |
Title |
|---|---|
10 |
Selfweight structure |
11 |
Prestress of superstructure |
15 |
Creep + Shrinkage |
20 |
Further permanent loads (for example asphalt) |
25 |
Creep + Shrinkage until traffic opening |
35 |
Creep + Shrinkage from traffic opening until t=oo |
List of Element Groups#
ID |
Title |
Element Type |
|---|---|---|
1 |
T-Beam left side |
BEAM |
2 |
T-Beam right side |
BEAM |
3 |
Area Elements Bridge Deck |
QUAD |
10 |
Support Elements Axis 10 |
SPRING, CONSTRAINT |
20 |
Support Elements Axis 20 |
BEAM, SPRING, CONSTRAINT |
30 |
Support Elements Axis 30 |
SPRING, CONSTRAINT |
Design code#
This tutorial is based on Eurocode EN 1992.
Starting a new project#
First we create a new SSD project and save it inside a project directory on your local computer. For further information see chapter Start New SSD Project in the General Workflow description.
Defining materials#
Generate all necessary materials listed above. Follow the procedures explained in chapter Material Definition in the General Workflow description.
Defining Cross Sections#
In this project we have only one standard cross section for the pier. Please generate a new cross section with the dimensions and material properties listed above. Follow the procedures explained in chapter Cross Section Definition in the General Workflow description.
The main bridge section will be defined graphically inside SOFiPLUS with the cross section editor.
Note
For the main bridge section we want to use a variable for the non effective parts of the cross sections. This variable will be defined within the bridge axis definition in SOFiPLUS. Therefore we recommend to create the bridge axis with all settings first.
Prestressing systems#
Please generate a new prestressing system number 1, with a VSL 6-19 multistrand system, see picture below.
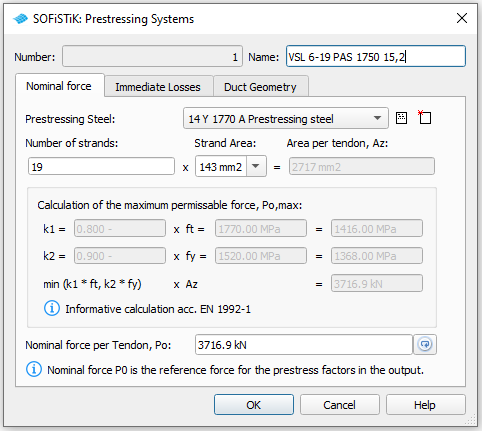
Follow the procedure explained in chapter Prestressing System in the General Workflow description.
System Generation in SOFiPLUS#
The bridge geometry will be defined using the CABD concept inside SOFiPLUS. For that we will work through the following steps:
Define main bridge axis
Define placements along the bridge axis
Define variables (will be used for the main cross section)
Define secondary axes with an offset. These axes are important for the bridge deck generation
Generate master cross section within Cross Section Editor
Generate structure lines representing the main T-beams
Generate structure areas representing the bridge deck
Use the Cross Members Editor to generate the support construction, containing piers, springs and couplings
Make a final check of the system and align elements if necessary
The following videos will show the main steps to generate the system.
Generate Bridge Axis#
First of all we define the main bridge axis, with placements, variables and secondary axes.
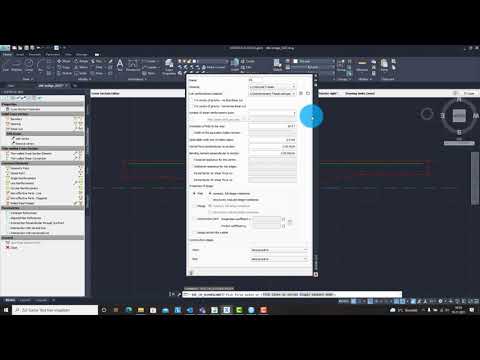
Generate Master Cross Sections#
For both T-beams we will define a master cross-sections inside SOFiPLUS. These master cross-sections contain cartesian references which use the variables #NEFFO and #NEFFI for the noneffective parts.
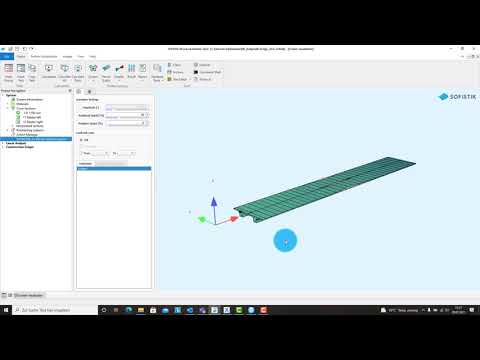
Generate Main T-Beams#
First we define the main T-beams. To do so, we simply switch of all secondary axis layers we do not need. In our case we keep the main axis and the secondary axes. Then we use the command “Line” from the tab “Structural Elements” in SOFiPLUS to create the T-beams.
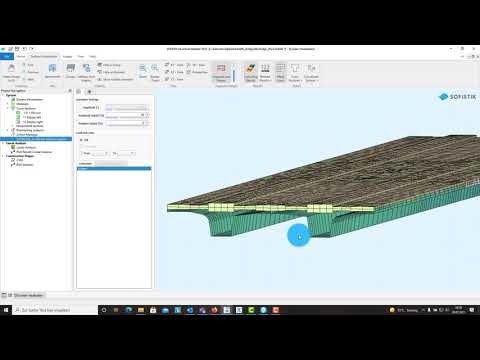
Generate Slab#
In the next step we will create the bridge deck. As the slab thickness varies over the width of the bridge we need to create that in several steps.
we switch on the necessary secondary axes
we create structural areas of group 3, with a constant thickness and with no geometric changes using the command “Segment on axis”
after that we modify the borders of the structural areas. With the AutoCAD feature “Isolate > Hide Objects” we can easily select the areas for the modification process
in the last step we change the geometry of the area elements: “Structural Area > Element Alingment > positive local z”
Note
In our system the area elements are supported by the T-beams. This means, that the span width in cross direction neglect the thickness of the T-beam web and results in a larger span width. One option to solve this problem is to define structural lines at the corner of the T-beam web and create a coupling between this lines and the T-beam. The following video will NOT show this modelling concept.
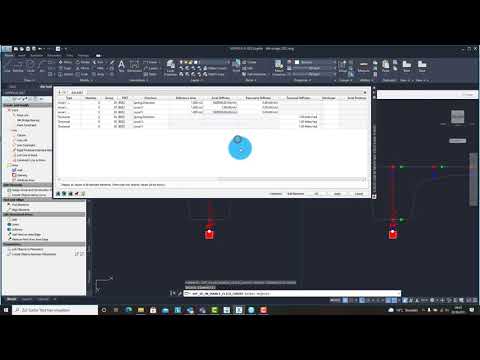
Generate Support Structure#
All supports will be created inside the Cross Members Editor. This allows you to work in the y-z-plane of the placement. All elements will be connected directly to the placement.
Generate Prestressing#
Please follow the procedures explained in our tutorial Post Tensioned Concrete Beam Bridge .
Loads#
The loads can be defined inside SOFiPLUS(-X). First define the necessary loadcases inside the Loadcase Manager. Then create the loads and allocate the loads to the loadcases. For details take a look at chapter Define Actions and Loads in the General Workflow description.
Linear Analysis#
All loads acting on the final bridge will be analysed with the task “Linear Analysis”. In our case we have a system with beam and area elements. This means, the stiffness of the area elements in the x-direction of the bridge is overlapping with the stiffness of the T-beams. Also the self weight of the area elements is overlapping with the T-beams. The self weight problem can be easily solved as we use a different concrete material with \(\gamma\) = 0 kN/m³ for the bridge deck (see also chapter “Bridge Materials”). The stiffness of the area elements can be reduced in the local x-direction by a special option of module ASE. The record GRP2 with the literals QUEA and QEMX allows us to reduce the membrane and bending action. With QUEA the E·A part of the QUAD elements and with QEMX the elastic modulus of QUAD elements can be modified in local x-direction. For that reason, we need to modify the task “Linear Analysis”. First we convert it into a “User Task” with the corresponding option in the right click menu.
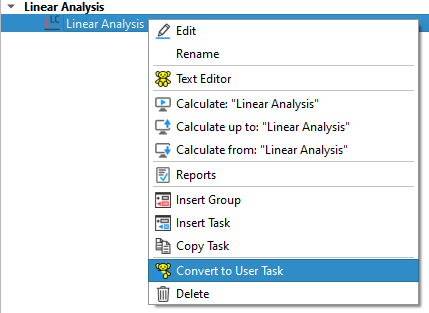
Then we add the new record GRP2 QUEA 0.01 QEMX 0.01 into the ASE module.
The input is printed below:
+PROG ASE $ Linear Analysis
HEAD Calculation of forces and moments
PAGE UNII 0
ECHO FULL FULL $ extensive output of text lists
CTRL OPT WARP VAL 0
CTRL OPT SPRI VAL 12
$ add record GRP2 to modify stiffness of QUAD elements
GRP2 NO 3 QUEA 0.001 QEMX 0.001 $ Reduce stiffness for bridge deck group 3
$ select loadcases to be analysed
LC 1,2
END
Construction Stage Manager#
The task “Construction Stage Manager” will be used as usual. Simply add this task and define all necessary stages. Inside the tab “Groups” it is necessary to create a new line for the bridge deck area elements, which is group 3 in our example. As done in the task “Linear Analysis” we need to reduce the stiffness properties of these elements. This can be directly done in the “Groups”-tab (see figure below).
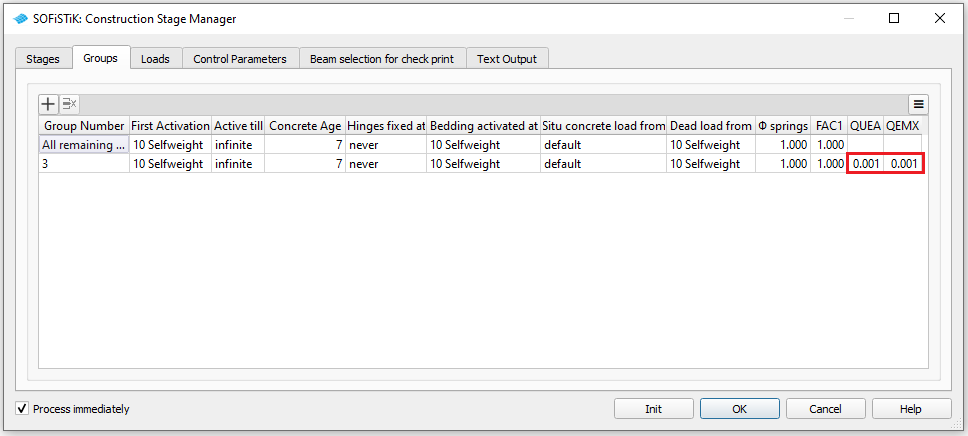
After that change we add the LC 2 with additional loads to the stage sequence in tab “Loads” and run the task. After the analysis finished, you should check the results with:
Report: Check the printout
Result: Check stresses inside cross sections for differnet load cases
GRAPHIC: Display and check the stress distribution of stress points along the bridge length
Traffic Loads#
The calculation of result envelopes with the Traffic Loader is basically done in the same way as described for the Post Tensioned Concrete Beam Bridge. One main difference is that we don’t have a single girder system here, but a hybrid system bulit of beam and shell elements (where the loads are distributed in cross-direction via the shell-elements). Therefore we have to choose a different setting to calculate the transverse load distribution based on transverse influence lines.
Set Shell-system: Transverse influence line with X interpolation points for the Transverse load distribution. You may choose between 3, 5, 7 or 9 interpolation points. More interpolation points generally lead to more exact results, however as a consequence this also consumes more computation time.
For the calculation of the transverse influence lines the information about wheel spacing and width of the load train is important. Therefore we also have to specify a load train for the evaluation: Set one of the defined LM1 load trains in this case.
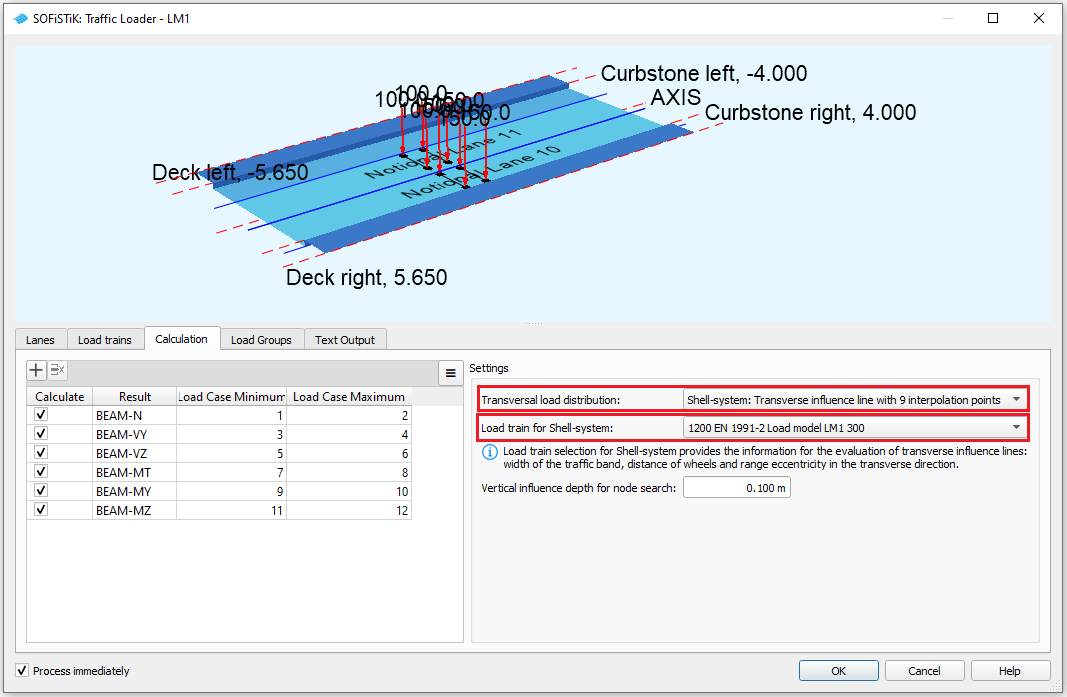
See also
In this tutorial we also want to offer you information about how to process special vehicles (LM3 acc. EN 1991-2) with the Traffic Loader. You will find a detailed description about it on the following page Special vehicles (LM3) with Traffic Loader.
Combinations#
Please follow the explanations of chapter Combinations and Superpositioning from the General Workflow description.
Design#
Please follow the explanations of chapter Design Checks from the General Workflow description.
Documentation#
For the final documentation, you can collect all single reports and generate a complete document. Please follow the explanations of chapter Generate Report from the General Workflow description.