Composite Bridge#
Introduction#
The idea of this tutorial is to guide you through a simple composite bridge project. We will introduce you to the general workflow for composite bridges and show the necessary program tools and functions. All steps like modelling, loading, traffic loads, combinations etc. are simplified.
We will focus on the design of the main beams. Design checks in transverse direction are omitted.
Note
A basic SOFiSTiK knowledge is required for this tutorial. The standard workflow is explained inside the General Workflow description. Inside this tutorial we show only the project specific workflows, which are different from the basic workflow.
Objectives#
Starting a new project
Define materials
Define cross sections
Generate system and loads inside SOFiPLUS
Generate traffic loads with load stepping method
Linear analysis
Construction stages
Combinations with CSM DESI
Plastic resistance moments
Calculation of stresses (including cracking of concrete)
ULS and SLS design checks
Calculation of longitudinal shear forces
Project description#
The geometry of the bridge model is based on a Eurocode design example (however for this tutorial we have strongly simplified it):
Note also that the loads used in our example differ from the load assumptions in the quoted document and that creep and shrinkage is processed in SOFiSTiK in a different way. Therefore it is not directly possible to compare hand calculations or results from the document with the results of the SOFiSTiK model.
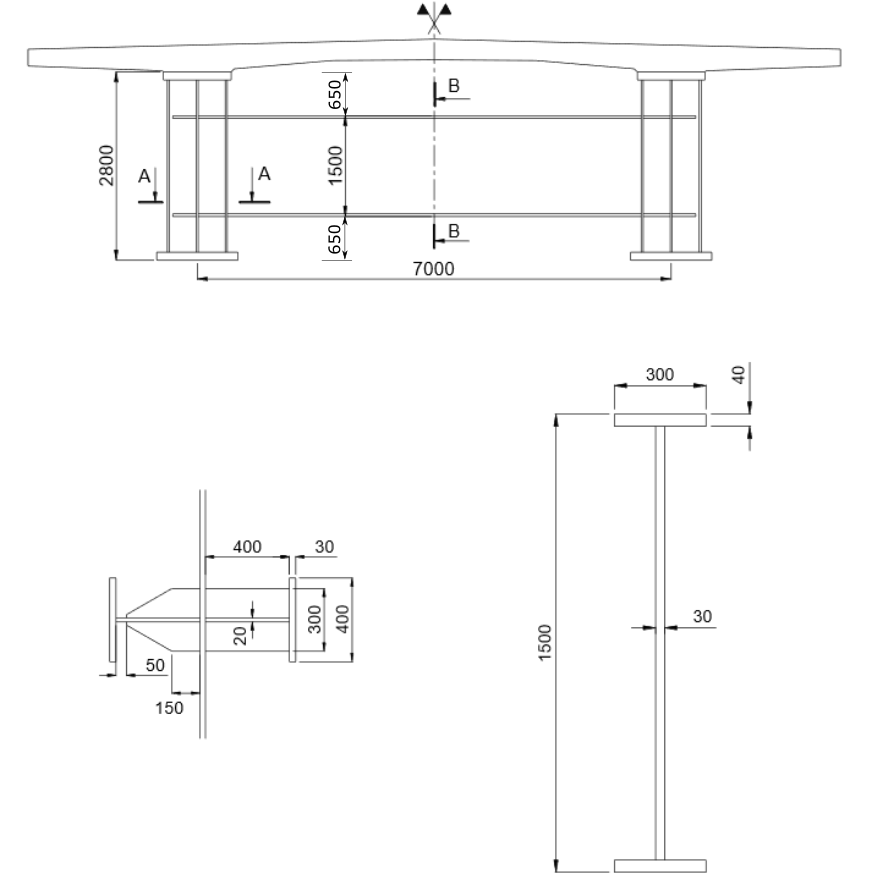
Side view

Typical span section
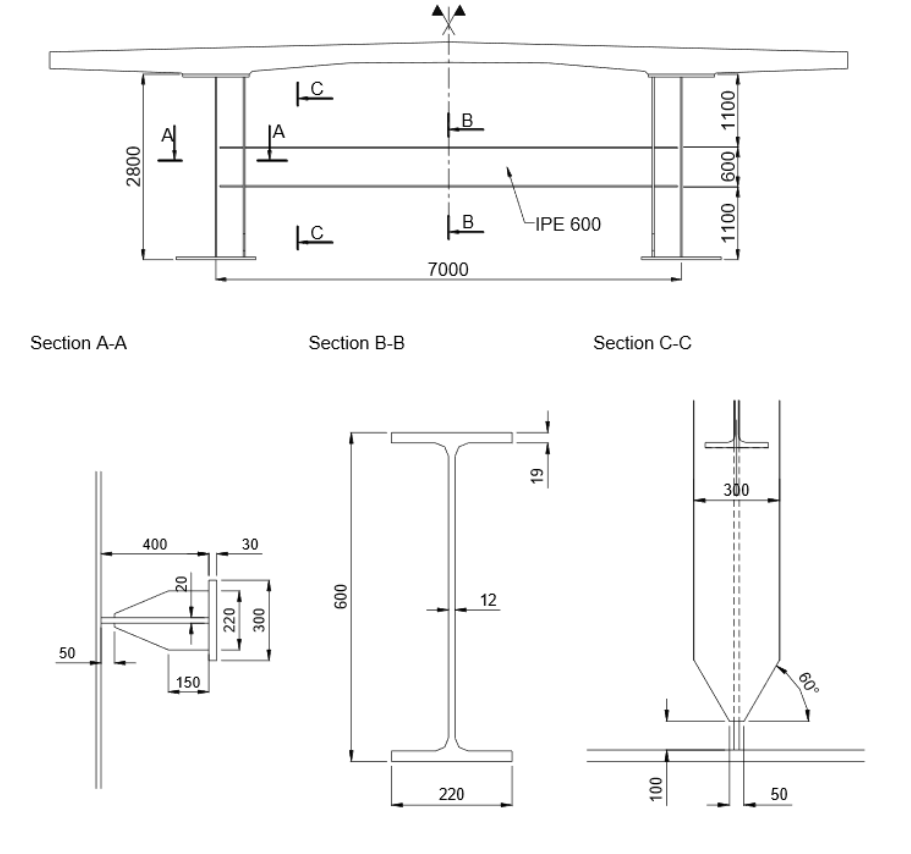
Typical support section
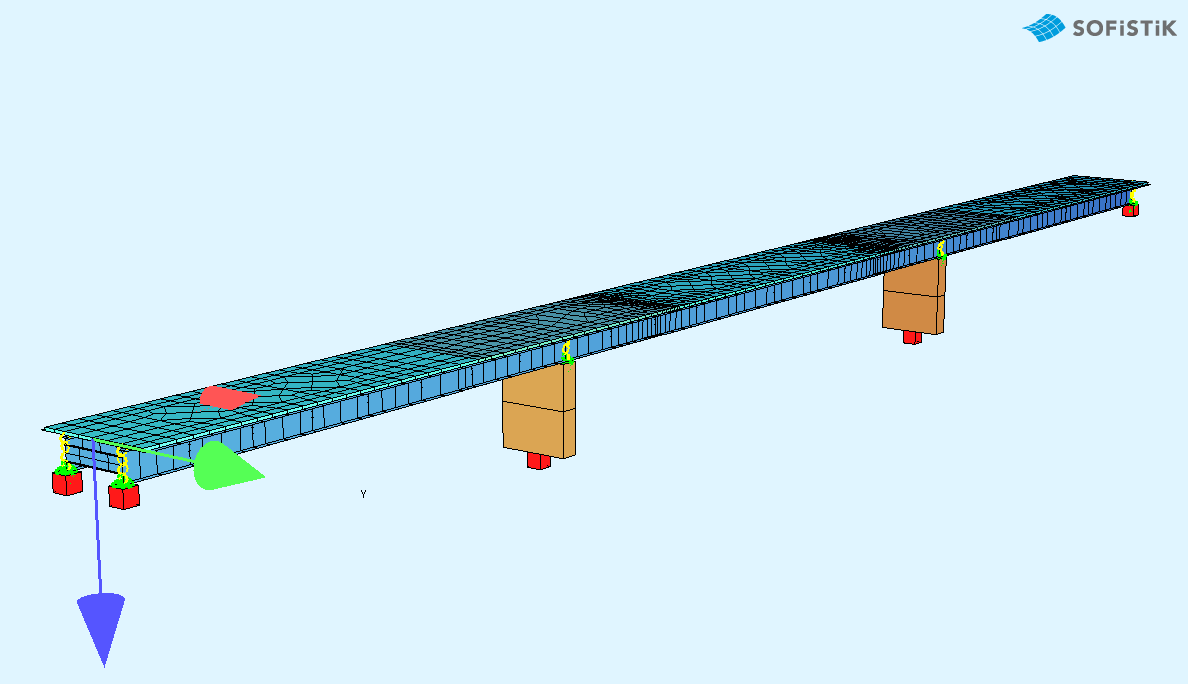
Overview bridge model
Bridge axis#
The bridge has 3 spans. In addition to the placements at the supports we also should define stations at points where a change of the cross-section takes place and at boundaries where the concrete is cast in different construction stages.
Spans [m] |
60.00 |
80.00 |
60.00 |
||||||||
Stations [m] |
0.00 |
43.00 |
60.00 |
77.00 |
123.00 |
140.00 |
157.00 |
200.00 |
|||
There are crossbeams at the supports, as well as every 7.50 m in the side spans and every 8.00 m in the central span.
Note
In this tutorial we use only two cross-sections per main beam (one for the spans and the other for the sections at the inner supports).
For simplicity we have summarized three aspects in the cross-setion change between span and support section:
a change in the structural steel cross-section (i.e. thickness of the sheets)
the concreting boundaries for the construction stages
the use of the cracked flexural stiffness at the inner supports to consider the cracking of concrete in the global analysis (based on EN 1994-2 5.4.2.3(2) resp. (3))
Generally we would have to define a station / new cross-section for each of these aspects, if these changes would not take place at the same position! Note also that due to this simplification the parts where we use a cracked flexural stiffness do not exactly match with the requirements of EN 1994-2 5.4.2.3(2) or (3)
Note
In the provided example file there are additional stations defined for the crossbeams. These are only important if you want to have a parametric model that automatically adapts to changes in the axes geometry. They are not mandatory for this tutorial.
Materials#
The following table shows the necessary materials.
Number |
Title |
Strength |
|---|---|---|
1 |
Structural steel |
S 355 |
2 |
Concrete composite beam uncracked |
C 35/45 |
3 |
Concrete composite beam cracked |
C 35/45, E = 300 N/mm² |
4 |
Reinforcement steel composite beam |
B 500 |
5 |
Shear connection |
S 355 |
10 |
Concrete slab - concreting section 1 (weightless) |
C 35/45, |
11 |
Concrete slab - concreting section 2 (weightless) |
C 35/45, |
20 |
Concrete piers |
C 30/37 |
Note
As we focus in this tutorial on the design of the main beams, we do not define reinforcement materials for the concrete slab (transverse direction) and the piers.
Cross-sections#
Number |
Title |
Dimensions |
|---|---|---|
1 |
Cross section span - left |
see figure below |
2 |
Cross section span - right |
see figure below |
3 |
Crossbeam - regular |
IPE 600 |
4 |
Crossbeam - supports |
I-profile: flanges b x t = 300 x 40, web h x t = 1420 x 30 |
5 |
Pier |
B x H = 8.000 m x 2.000 m |
10 |
Cross section support - left |
see figure below |
20 |
Cross section support - right |
see figure below |
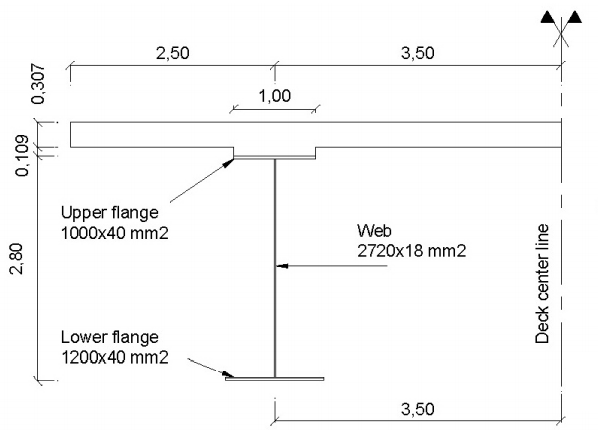
Cross-section span (simplified)
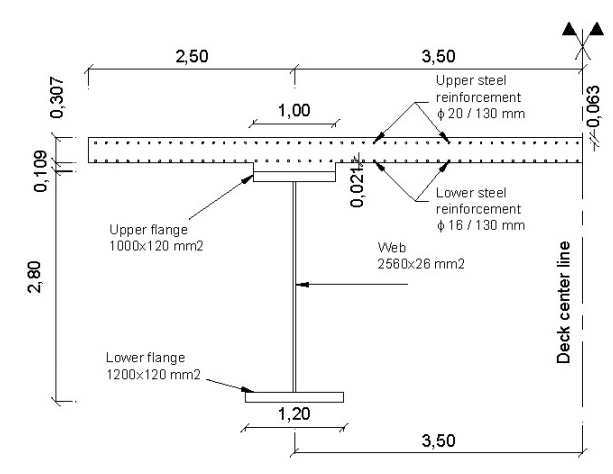
Cross-section support (simplified)
Construction stages#
Stage Number |
Title |
|---|---|
10 |
Formwork steel beams |
19 |
Wet concrete - span sections |
20 |
Concrete stiffness - span sections |
25 |
Creep + Shrinkage |
29 |
Wet concrete - support sections |
30 |
Concrete resp. Reinforcement stiffness - support sections |
35 |
Creep + Shrinkage |
40 |
Additional permanent loads (e.g. asphalt, bridge equipment) |
45 - 50 |
Creep + Shrinkage from traffic opening until t=oo |
List of element groups#
ID |
Title |
Element Type |
|---|---|---|
1 |
Composite T-Beam left side |
BEAM |
2 |
Composite T-Beam right side |
BEAM |
3 |
Crossbeams |
BEAM |
4 |
Piers |
BEAM |
10 |
Area elements bridge deck - span section |
QUAD |
20 |
Area elements bridge deck - support section |
QUAD |
30 |
Support Elements |
SPRING, CONSTRAINT |
Design code#
This tutorial is based on Eurocode DIN EN 1994.
Starting a new project#
First create a new SSD project and save it inside a project directory on your local computer. For further information see chapter Start New SSD Project in the General Workflow description.
Define materials#
Generate all necessary materials listed above. The general procedure is explained in chapter Material Definition in the General Workflow description. For the composite bridge we have to take care of the following modifcations:
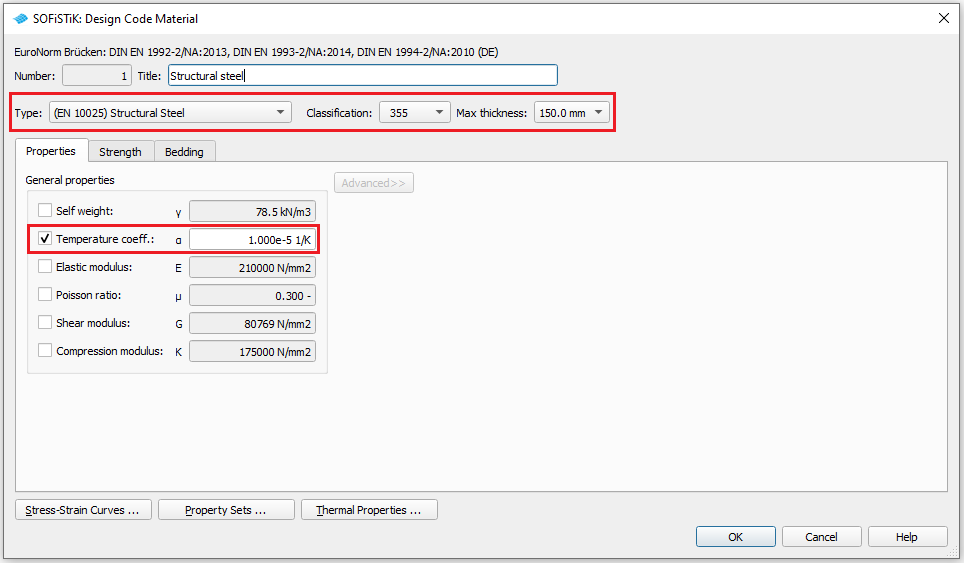
According to DIN EN 1994 5.4.2.5 (3) we set the thermal expansion coefficient for structural steel to = 10e-6 /K.
Note that for the computation of the deflections at the supports, which is not covered in this tutorial,
different settings may be required.
Note
The flanges of the support section have a thickness of t = 120 mm. Therefore we have to create a steel material, which allows such a thickness for the sheets.
This can be done by choosing in the task “Design Code Material” as “Type” (EN 10025) Structural Steel and setting the the tab “Max thickness” accordingly.
For the design tasks you should be aware that a steel S 355 with this setting has a yield strength of only 295 N/mm².
For simplicity we do not define an additional steel matertial for the other sheets with a thickness t 40 mm (allowing a yield strength fy = 355 N/mm²).
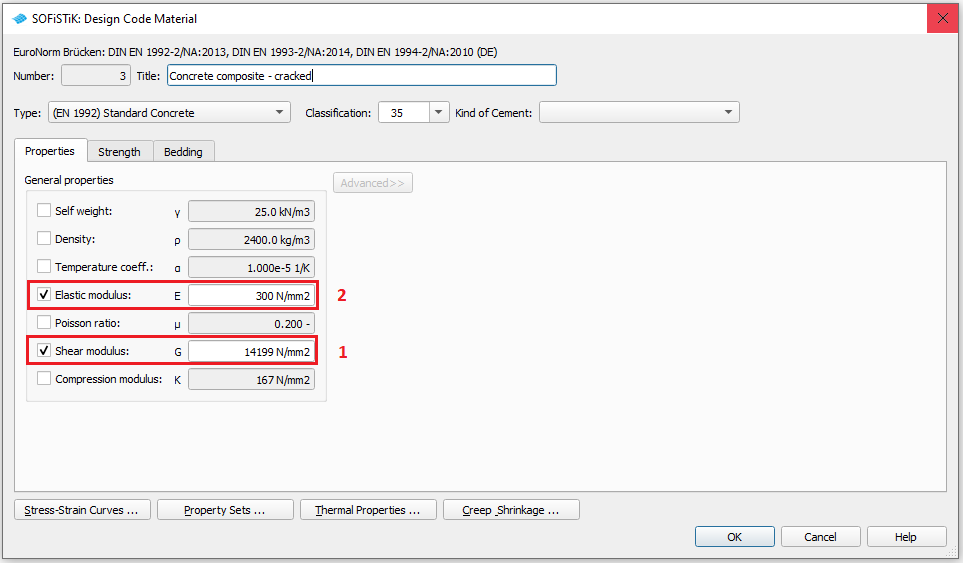
The effect of cracking of concrete at the inner supports can be considered in the global analysis according to DIN EN 1994 5.4.2.3 (2) resp. (3) by using the bending stiffness of the cracked composite section in the areas adjacent to the supports. For this we define a second concrete material with a reduced elastic modulus of E = 300 N/mm².
Important
In case that you want to reduce the elastic modulus E, please take into account that the shear modulus G will be reduced automatically as well. First set the shear modulus G as fix and then change the elastic modulus E. See figure below how to do it in the dialog “Design Code Material”.
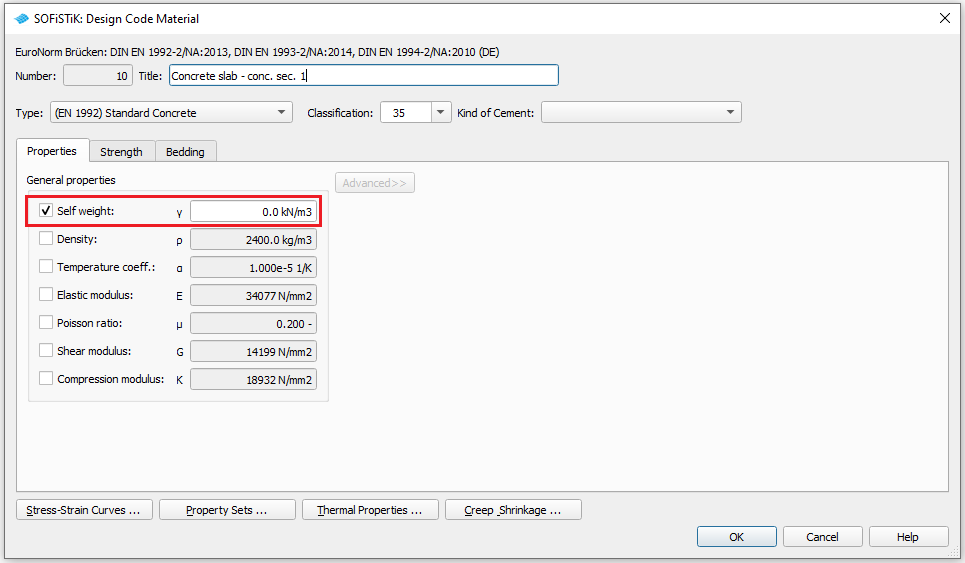
Because the self weight of the concrete slab will be accounted for by the concrete parts of the main beams,
we set the self weight of the concrete materials of the slab (material nr. 10 and 11) to = 0 kN/m².
Define standard cross sections#
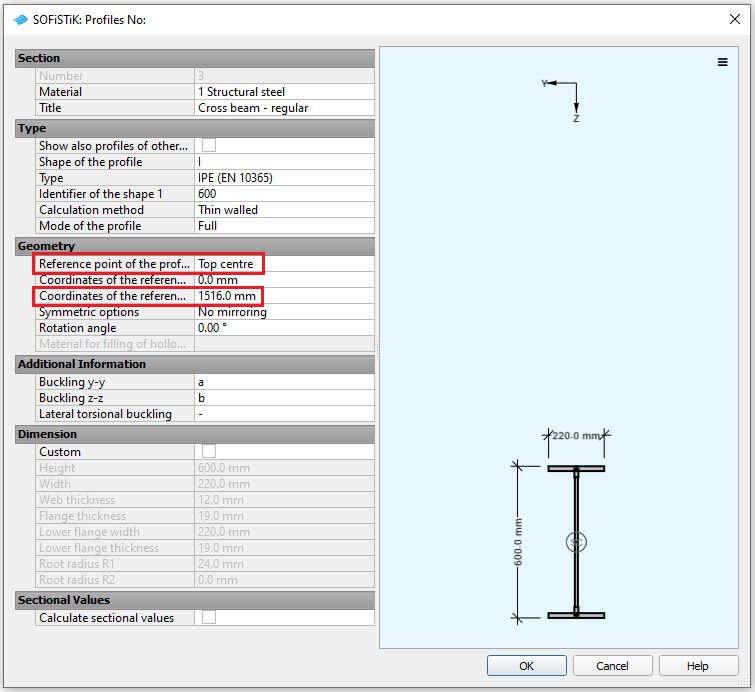
In this project we have three standard cross sections (regular crossbeams, crossbeams at supports and pier). Please generate the cross sections with the dimensions and material properties listed above. The general procedure is outlined in chapter in Cross Section Definition of the General Workflow description.
The crossbeams are positioned in vertical direction in mid height of the steel part of the main beams. Take care to set the coordinates of the reference point for the crossbeams for a correct positioning in the model.
The main bridge section will be defined later graphically inside SOFiPLUS with the cross section editor.
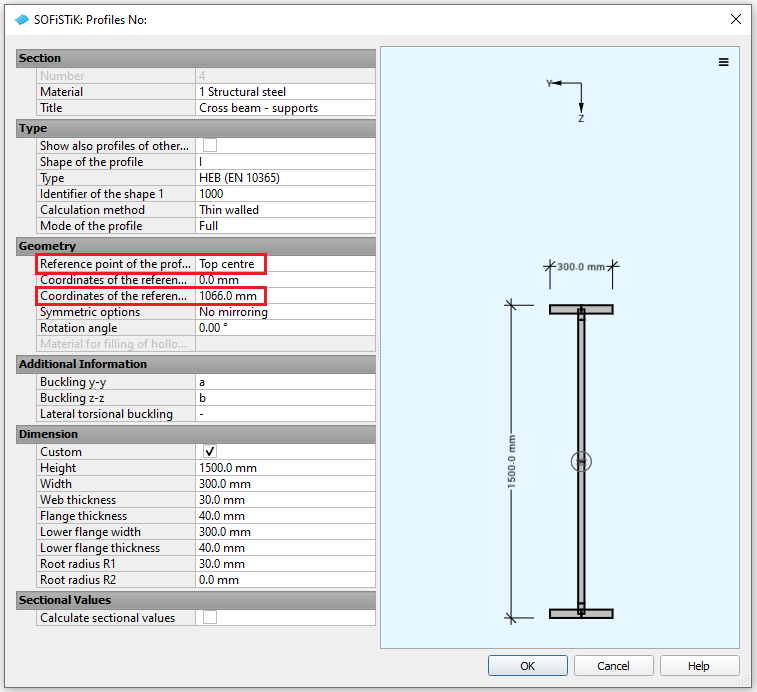
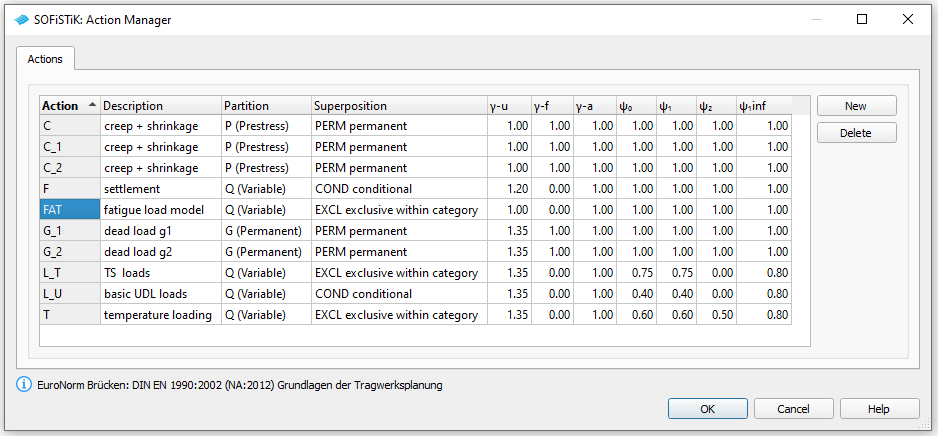
Actions#
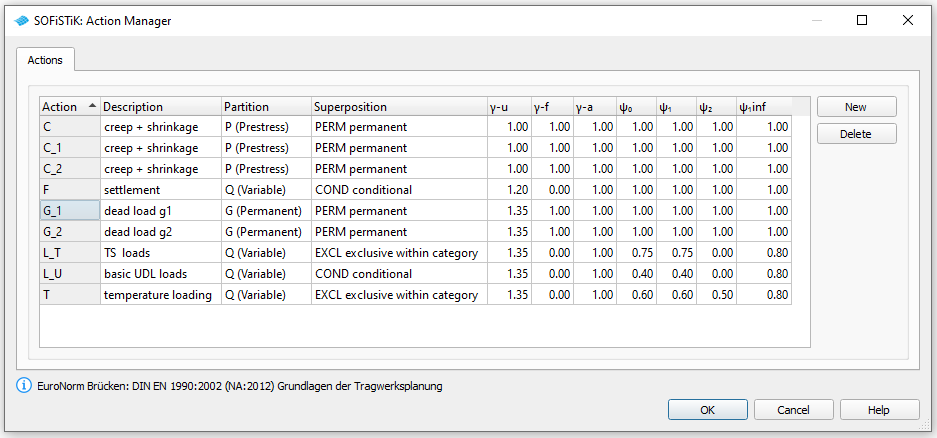
Before we define any load, we must define all necessary actions within the SSD “Action Manager”. In our bridge example we need the following actions.
System generation in SOFiPLUS#
Bridge axis#
Generate the main bridge axis including secondary axis based on the geometry information from the project description. How to do this is for example shown in section “Generate Bridge Axis” of our tutorial “Double T-Beam Post Tensioned Concrete Bridge”.
In this tutorial you will need secondary axes with “Offset Y” = -3.5 m and “Offset Y” = 3.5 m for the main beams and with “Offset Y” = -6.0 m and “Offset Y” = 6.0 m for the generation of the slab.
Note
For a general step-by-step explanation how to generate a bridge geometry you can also take a look at our Computer Aided Bridge Design (CABD) training videos.
in englisch: https://www.youtube.com/watch?v=ModT1vB5pS8
in german: https://www.youtube.com/watch?v=txV3WQodxkQ
Cross-sections#
In this tutorial we will define the cross-sections in SOFiPLUS(-X) using the Cross Section Editor. Generally following steps are necessary for the definition of composite cross sections:
Make sure all necessary materials are defined first
Define variables to be used inside the cross section first within the axis definition (not covered by this tutorial)
Define cross section properties
Draw geometry
Define cross-section elements and reinforcement
Define stress points
In general composite cross-sections can be modeled either as “solid” or as “thin-walled” cross-sections. Each modelling approach has advantages but also drawbacks with regard to modelling and evaluation, which are summarized in following table (for more details see also manual of module “AQUA”):
solid |
thin-walled |
|
|---|---|---|
definition steel part |
polygonal definition: points have to be defined in every corner of the steel profile |
thin-walled elements (sheets) are defined via a start and end point |
definition concrete part |
polygonal definition: shape of the concrete cross-section can be modeled exactly |
defintion via wall elements with constant thickness: shape of concrete slab has to be simplified |
definition of shear connection between steel and concrete |
automatically via contact between steel and concrete areas |
via element “shear connection” |
computational effort |
higher effort, because fine discretization for FEM analysis of cross-section necessary |
less effort |
prerequisits for correct evaluation of c/t-checks |
additional stress points necessary to define “start” and “end” point of each sheet |
no additional input necessary: boundary of each sheet given by start and end point of thin-walled element |
Note
To reduce the computational effort for solid cross-sections it is generally possible to change the analysis type for the cross-section (default CTRL STYP FEM, see also manual of module AQUA). Be aware that a change of the default settings can affect the accuracy of your results.
For standard composite cross-sections we recommed to use “thin-walled” cross-sections. The following video shows the generation of cross section 1 from this tutorial example.
Create the other composite cross-sections in the same way. Take care to set for the support cross-sections the “cracked” concrete material number 3 and to define and use construction stage number 30 for the concrete parts and the reinforcement.
Important
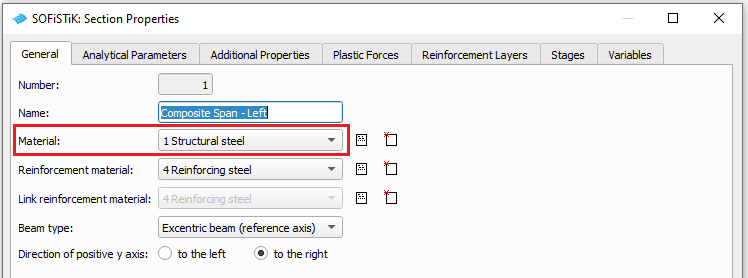
We strongly recommend to use the structural steel material as reference material for composite cross-sections as shown in the video.
Important
By default the torsional moment of inertia for composite cross-sections is computed considering both steel and concrete part of the cross-section. For systems similar to the double T-beam example in this tutorial we recommend to set the torsional stiffness for composite cross-sections manually and use the torsional stiffness of the steel profile only as shown in the video. The reason is that without this setting small rotations around the longitudinal direction of the bridge (for example resulting from a difference in the deflection of the main beams due to unsymmetric traffic loading) would lead to big torsional momemts in the main beams due to their high torsional stiffness. For the computation of the design shear stresses later on we want to assign the torsional moments and shear forces to the steel profile only (see section “Nonlinear computation” in chapter “Design checks for the ultimate limit state”). We then would assign a torsional moment that has been computed for a stiff cross-section to a cross-section that is more flexible and has a much lower bearing capacity for torsional moments. Due to this inconsistency we would get unrealistic high shear stresses and warnings that the cross-section can not bear the assigned loads.
Warning
In this tutorial we use an extra material (nr. 5) for the “Thin-walled Shear Connection”. Be aware that this feature is only provided from SOFiSTiK Version 2020 onwards and will trigger an error message in older versions. In version 2018 or older you have to use a material that is already applied in the cross-section (i.e. structural steel or concrete material) for the shear connection.
Important
For composite cross-sections we strongly recommend to define a realistic amount of reinforcement and carry out the design checks based on the computed stresses and not as it is common in most reinforced concrete workflows to define a minimum reinforcement and calculate the necessary amount of reinforcement in the design procedure. In the basic example file for this tutorial we define the amount of reinforcement directly in the cross-section definition for each cross-section individually. If you have varying amounts of reinforcements along the bridge axis and you do not want to define an individual master cross-section for each reinforcement change we show you an alternative possibility in the last chapter of this tutorial.
Beam elements#
After having defined all necessary cross-sections you can generate the beam elements for the system. Take a look at the section “Generate Main T-Beams” of our tutorial “Double T-Beam Post Tensioned Concrete Bridge” for the procedure.
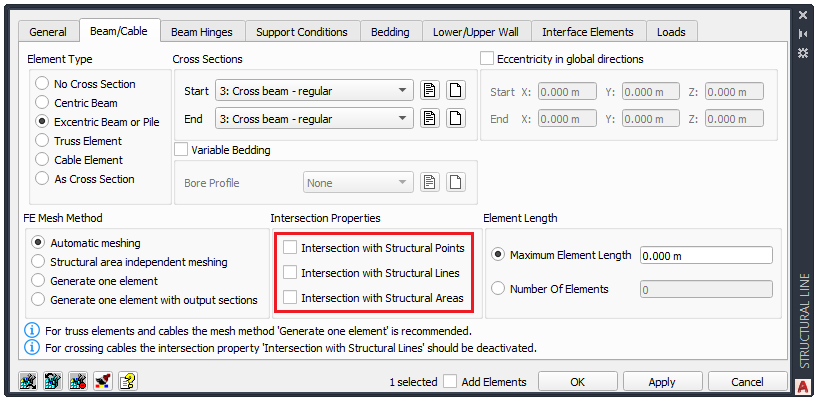
The crossbeams are no composite beams and should not be connected to the concrete slab (which we will define in the next section). Therefore it is important to deselect all intersection properties for the cross-beams as displayed in the sequel.
Concrete slab#
Generate the concrete slab. The general procedure how to do it is shown in the section “Generate Slab” of the “Double T-Beam Post Tensioned Concrete Bridge” tutorial. To simplify the generation of the slab we do not take into account haunches and model it with constant thickness of 307 mm.
Support elements#
Generate the support elements and the piers. Take a look at the section “Generate Support Structure” of the tutorial “Double T-Beam Post Tensioned Concrete Bridge” how to do this.
Loads#
We will define additional permanent loads (e.g. asphalt, bridge equipment), basic temperature loads and settlements in SOFiPLUS(-X). First define the necessary loadcases inside the “Loadcase Manager”.
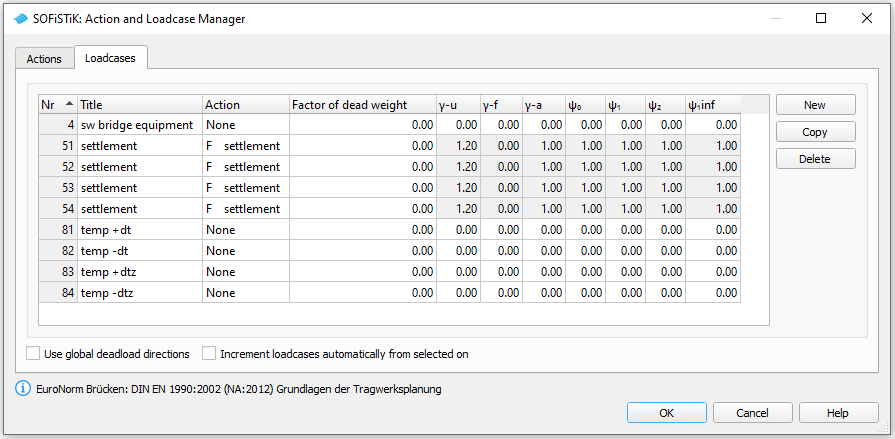
Important
Load cases which will be used later on inside the CSM should be saved within the action container NONE. With this concept the load cases will not be used twice in case the user defines his own combination rules using actions only!
After defining the loadcases we generate the loads in SOFiPLUS(-X) and allocate them to the loadcases.
Note
For a step-by-step explanation how to generate loads for beams in SOFiPLUS(-X) you can also take a look at our corresponding CABD training videos.
in englisch: https://www.youtube.com/watch?v=uSGGvvpd-YE
in german: https://www.youtube.com/watch?v=fwVo8RpTH1w
Define additional dead loads (bridge equipment). Use a area load of 2.5 kN/m² in direction of the self weight for the complete area of the concrete slab (asphalt) and line loads of 1.5 kN/m at the left and right boundary of the slab (railing).
Define a settlement wzz = 10 mm at every support axis and save the loads within the load cases 51 to 54.
For the temperature loads we generate 4 loadcases 81 to 84 containing the basic temperature loads.
LC |
Action |
Designation |
|---|---|---|
81 |
NONE |
constant temperature DT = + 31°C |
82 |
NONE |
constant temperature DT = - 30°C |
83 |
NONE |
temperature difference DTZ = 15°C (top warmer) |
84 |
NONE |
temperature difference DTZ = -18°C (bottom warmer) |
Note
In SOFiSTiK a positive sign for the lineare temperature difference corresponds to an increase of temperature in positive z- (resp. y-) direction. Depending on the direction of the local coordinate system of the cross-section the correct sign for temperature differences can differ from the definitions given in EN 1991-1-5.
See also
The definition of the temperature difference above is based on vertical linear components (approach 1) according to EN 1991-1-5 6.1.4.1. Alternatively a second method (approach 2) with nonlinear temperature difference components is specified in EN 1991-1-5 6.1.4.2. For more information about the usage of loadcases with nonlinear temperature differences, see the following page Nonlinear temperature.
Combination of temperature#
For the combinations of temperature loads according to the specifications in EN 1991-1-5 6.1.5 please see chapter Define Actions and Loads of the General Workflow description.
Traffic loads#
In this tutorial we evaluate the traffic loads using the “Load Stepping Method”. As we focus on the design checks for composite bridges, we will simplify the load definition by evaluating in transverse direction only one load position (giving the decisive loading for the left main beam).
Load Case Numbering#
LC |
Action |
Designation |
|---|---|---|
100 |
NONE |
load train LM1 - lane 1 (300 kN axle load) |
101 |
NONE |
load train LM1 - lane 2 (200 kN axle load) |
102 |
NONE |
load train LM1 - lane 3 (100 kN axle load) |
200 - 202 |
L_U |
load stepping UDL; 3 spans |
300 - 340 |
L_T |
load stepping TS |
Workflow Load Stepping Method#
The following steps are necessary to define the traffic loads:
Define lanes using the following text input:
+PROG SOFILOAD
HEAD Define lane
LANE MAIN TYPE EN WL -5.50 WR 5.50 YLA -6.00 YRA 6.00 $$ $ define lane
SA 0.00 SE 60.00 $ define span 1
SA 60.00 SE 140.00 $ define span 2
SA 140.00 SE 200.00 $ define span 3
END
Define load trains. The loads are saved in the following load cases:
+PROG SOFILOAD
HEAD Define load trains
ECHO LOAD EXTR
LC 100 TYPE NONE $ lane 1
TRAI LM1 300
LC 101 TYPE NONE $ lane 2
TRAI LM1 200
LC 102 TYPE NONE $ lane 3
TRAI LM1 100
END
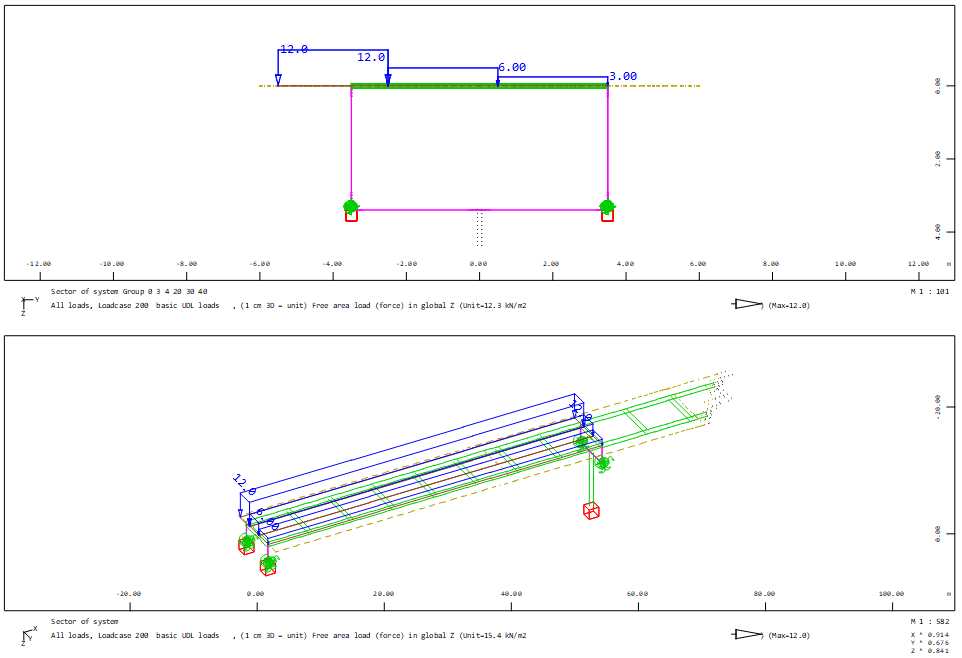
Generate a series of load cases for UDL loads (for simplicity here only most left transverse position):
+PROG SOFILOAD
HEAD Load stepping LM1 UDL
LOOP#K 3
LC 200+#K TYPE L_U ; COPY 100 REF 'MAIN.20' DX 0 WIDE 1 from 1+#K to - inc 0 type gru0
COPY 101 REF 'MAIN.21' DX 0 WIDE 1 from 1+#K to - inc 0 type gru0
COPY 102 REF 'MAIN.22' DX 0 WIDE 1 from 1+#K to - inc 0 type gru0
ENDLOOP
END
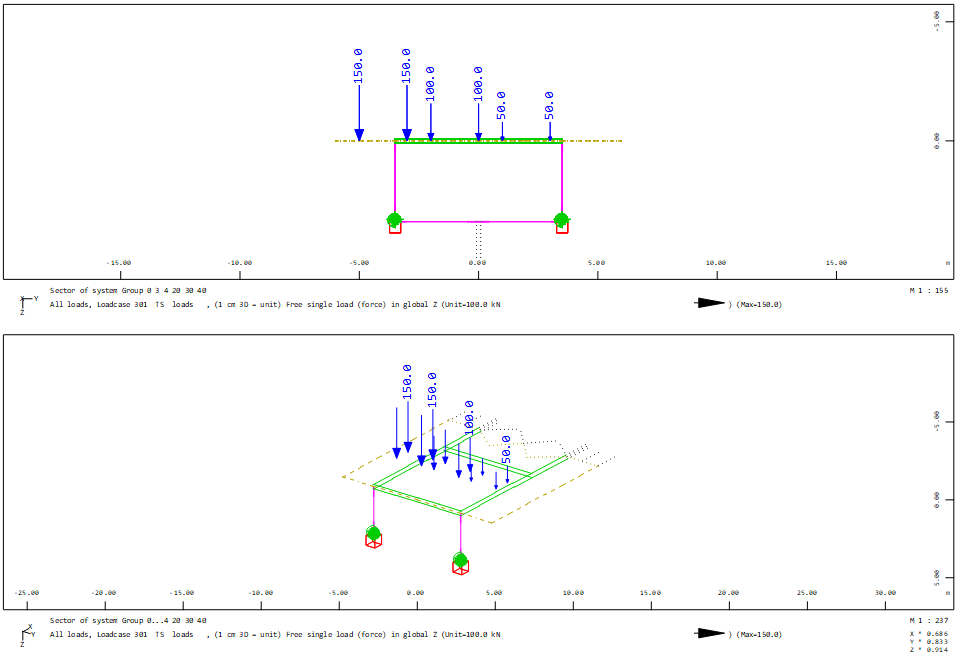
Generate a series of load cases for TS loads (for simplicity here only most left transverse position):
+PROG SOFILOAD
HEAD Load stepping LM1 TS
LET#DX 5
LET#X 0.6
LOOP#I 41
LC 300+#I TYPE L_T ; COPY 100 REF 'MAIN.20' DX #X WIDE 1 type gr0
COPY 101 REF 'MAIN.21' DX #X WIDE 1 type gr0
COPY 102 REF 'MAIN.22' DX #X WIDE 1 type gr0
LET#X #X+#DX
ENDLOOP
END
Linear Analysis#
All loads acting on the final bridge will be analysed with the task “Linear Analysis”. In our case we have a system with composite beams and area elements. We have defined the area elements to model the stiffness of the concrete slab in transverse direction. The stiffness of the slab in longitudinal direction (x-direction) is already covered by the concrete parts and the reinforcement of the composite beams. Therefore we have to reduce the stiffness of the area elements in the local x-direction (otherwise we would account for the stiffness of the concrete twice). This can be done by a special option of module ASE using the command GRP2 with the literals QUEA and QEMX. With QUEA the normal force stiffness component and with QEMX the elastic modulus of QUAD elements in local x-direction can be modified.
For this you can create a task “Linear Analysis” as described in the chapter Linear Analysis of the General Workflow description, convert it into a “User Task”, add the GRP2 QUEA QUEMX command and set the respective QUAD stiffness parts to 1% of their original value. The resulting command block looks like this:
+PROG ASE $ Linear Analysis
HEAD Calculation of forces and moments
PAGE UNII 0
CTRL OPT WARP VAL 0
CTRL OPT SPRI VAL 12
GRP2 NO 20,30 QUEA 0.01 QEMX 0.01 $ Reduce the QUAD-stiffness in longitudinal direction
LC (51 54 1)
LC (81 84 1)
LC (91 98 1)
LC (200 202 1)
LC (300 340 1)
END
Construction Stage Manager#
For the computation of the permanent loads and creep and shrinkage effects we use the “Construction Stage Manager (CSM)”. A basic description of the CSM workflow is given in chapter Construction Stages of the General Workflow tutorial. For our composite example following steps are important:
Define the construction stages given in the project description.
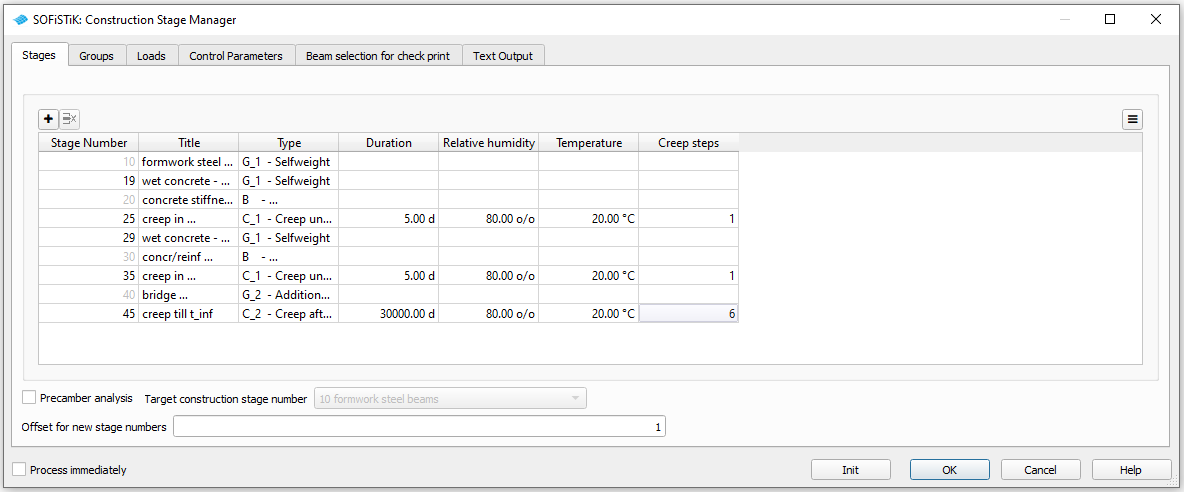
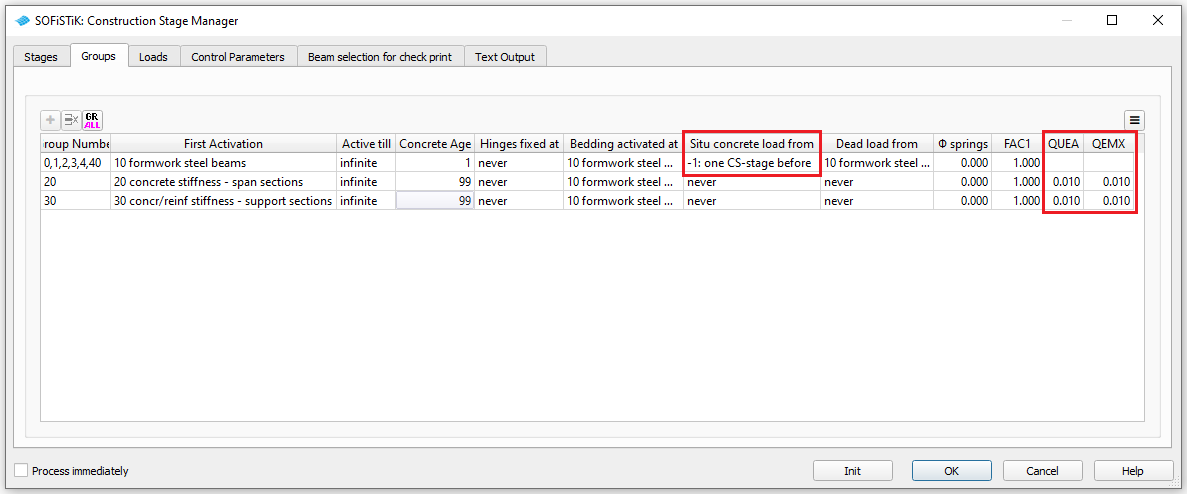
Define the properties and activation stages for the element groups. Set the situ concrete load for the main beams (group 1, 2) to -1. So the self weight of the in-situ concrete is activated one construction stage earlier than the stiffness of the concrete. For this feature it is essential that the construction stages where the loads will be applied are defined (in our case the constrcution stages 19 and 29 as the activation of the concrete stiffness happens in construction stage 20 resp. 30) and the automatic activation of the self weight is enabled (see below).
As in the Linear Analysis task we have to reduce the stiffness of the QUAD elements in longitudinal direction. This can be directly done in the tab “Groups”.
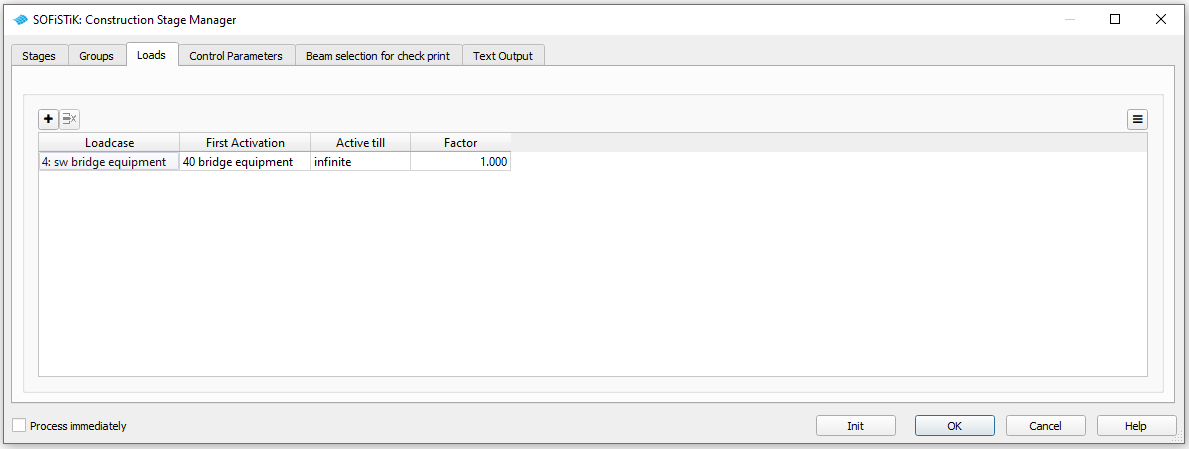
Define additional loads. Here only the permanent loads from the bridge equipment (defined in SOFiPLUS) have to be activated.
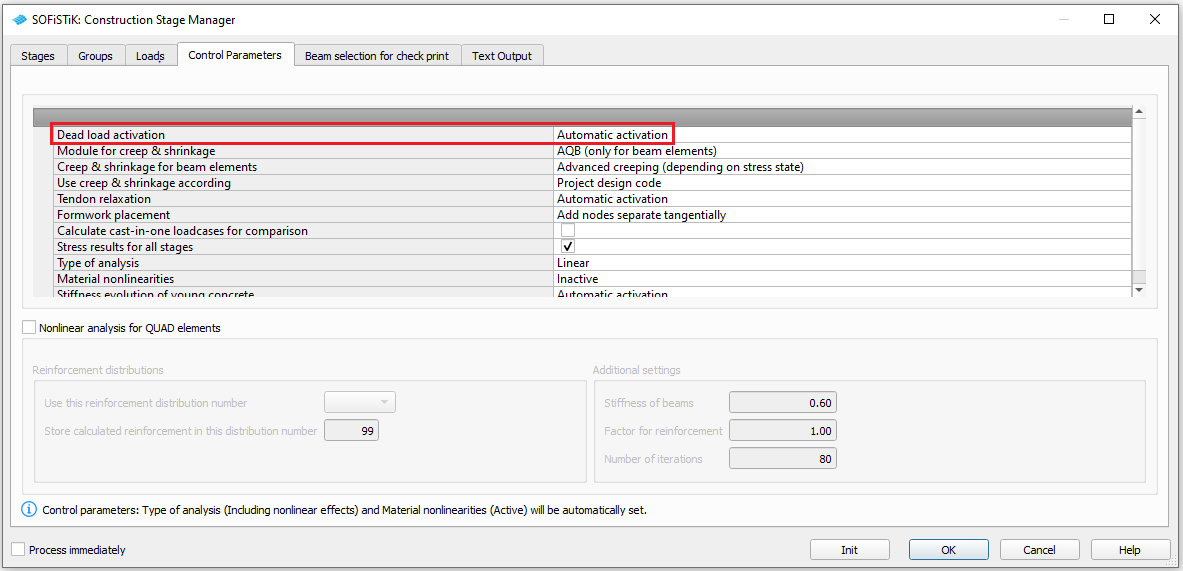
For the application of the self weigth of the structural elements we use “automatic activation”, which can be set in the tab “Control Parameters”.
The eigenstresses due to creep and shrinkage are computed by the module AQB. The current default setting for AQB is not to take into account the reinforcement for the computation of eigenstresses, because a later increase of the reinforcement (as usually done in most reinforced / prestressed concrete workflows) would violate the equilibrium of the internal stresses.
However for our composite bridge we will not change the reinforcement and want to take it into account for eigenstresses from creep and shrinkage. To enable this we have to convert the task “Construction Stages” into a “User Task” and add the command CTRL AQB TEXT ‘CTRL EIGE -64’.
+PROG CSM urs:12 $ Construction Stages
HEAD Calculation of Construction Stages
PAGE UNII 0
CTRL AQB TEXT 'CTRL EIGE -64' $ consider reinforcement for computation of eigenstresses
CTRL OPT DL VAL AUTO
CTRL OPT BEAM VAL AQB
CTRL OPT CREP VAL RCRE
CTRL OPT RELZ VAL AUTO
CTRL OPT CANT VAL 12
CTRL OPT CAST VAL 0
CTRL OPT STOR VAL 1
CTRL OPT PROB VAL LINE V2 80
CTRL OPT NMAT VAL NO
CTRL OPT EMOD VAL AUTO
CTRL OPT GPCS VAL 0
$ Table of Construction Stages
CS 10 TYPE G_1 TITL 'formwork steel beams '
CS 19 TYPE G_1 TITL 'wet concrete - span sections'
CS 20 TYPE B TITL 'concrete stiffness - span sections'
CS 25 TYPE C_1 TITL 'creep in construction' T 5 RH 80 TEMP 20 NCRE 1
CS 29 TYPE G_1 TITL 'wet concrete - support sections'
CS 30 TYPE B TITL 'concr/reinf stiffness - support sections'
CS 35 TYPE C_1 TITL 'creep in construction' T 5 RH 80 TEMP 20 NCRE 1
CS 40 TYPE G_2 TITL 'bridge equipment'
CS 45 TYPE C_2 TITL 'creep till t_inf' T 30000 RH 80 TEMP 20 NCRE 6
$ Table of Groups
GRP 0,1,2,3,4,40 ICS1 10 ATIL - HFIX 99999 BEDD 10 SITU -1 T0 1 FAC1 1 ICSD 10 PHIF 0
GRP 20 ICS1 20 ATIL - HFIX 99999 BEDD 10 SITU 99999 T0 99 FAC1 1 ICSD 99999 PHIF 0 QUEA 0.01 QEMX 0.01
GRP 30 ICS1 30 ATIL - HFIX 99999 BEDD 10 SITU 99999 T0 99 FAC1 1 ICSD 99999 PHIF 0 QUEA 0.01 QEMX 0.01
$ Table of Loads
LC 4 ICS1 40 ATIL - FACT 1
END
+apply "$(NAME)_csm.dat"
Combinations#
To calculate the design combinations insert the task “CSM Bridge Design - Superpositioning”
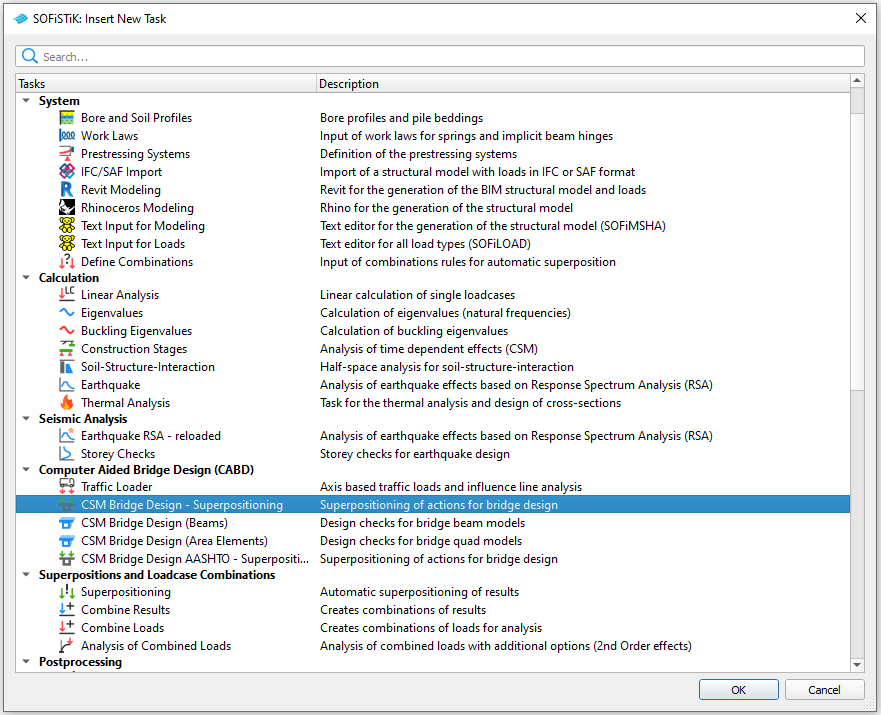
In the task you can select the actions for the superpositioning. Please note that you only have to select the actions for variable loads. The permanent actions, e.g. selfweight, additional dead loads (G, G_1, G_2, …) and creep and shrinkage (C, C_1, C_2, …) are considered automatically according to the loadcases created by the “Construction Stage Manager”.
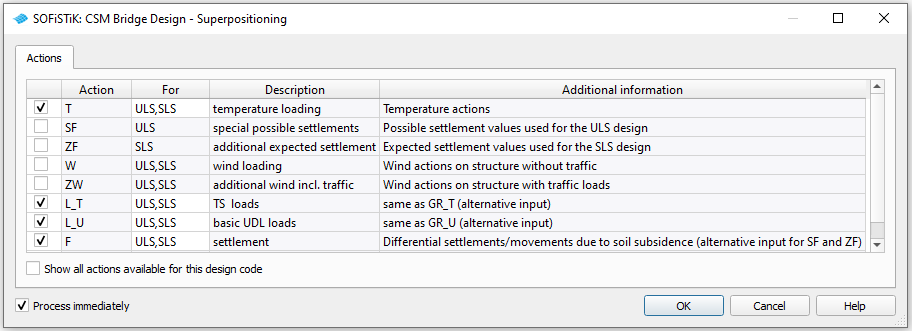
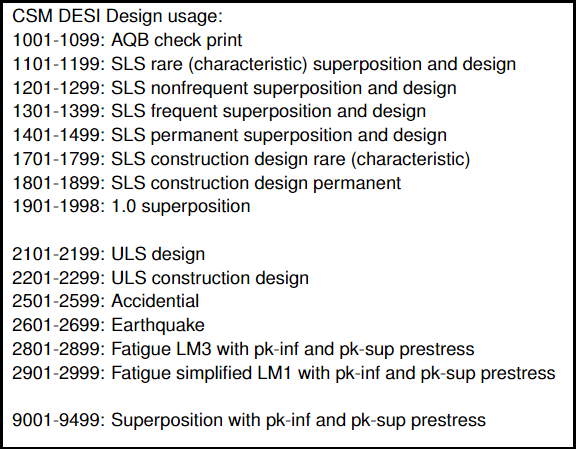
For the loadcases created by the CSM with DESI MAXI take a look at the manual of module CSM (see following excerpt). Note that for our composite bridge tutorial (i.e. no prestress) and the defined actions not all the listed superpositions will be created.
Design checks for ultimate limit state#
SOFiSTiK provides several tools to carry out the computation of stresses and the design checks. Depending on the application the user has to choose the appropriate tool and be aware of the capabilities and limits of the software.
In the sequel we will show the most important tasks / commands and discuss what they can and can not do.
Important
In the current workflow all design checks that have to do with stability and buckling are omitted. Stability checks especially regarding the possibility of lateral torsional buckling (DIN EN 1994-2 6.4) have to be checked by the user based on the computed forces. A reduction of the design resistance due to buckling according to EN 1993-1-5 is not considered in the utilisation factors computed in this tutorial. Design checks for cross-sections classified in class 4 and the corresponding design of stiffeners have to be carried out by the user seperately based on the calculated stresses.
Note
We have defined the structural steel of type “S 355” with a maximum allowable thickness of 150 mm (see also section “Define materials”). Keep in mind that with this specification steel “S 355” has a yield strength of only 295 N/mm², if you check the utilisation factors and cross-section resistance in this tutorial.
Note
The bridge example used in this tutorial has originally been designed according to the french national annex of the Eurocodes. In the present example we have set up the loading and the design checks according to the german national annex. Due to the higher traffic loads required by the NAD the design checks are not always met (i.e. utilisation factor > 1.0).
Plastic resistance moments#
The cross-sections resp. their properties are stored in the database after their definition and export in SOFiPLUS. To check the cross-sectional values we can compute the task “Cross-Sections” in the SSD and take a look at the generated report file.
We can have a look at the cross-section properties in the created report file as shown in the video in the chapter “System generation in SOFiPLUS” - “Cross-sections”.
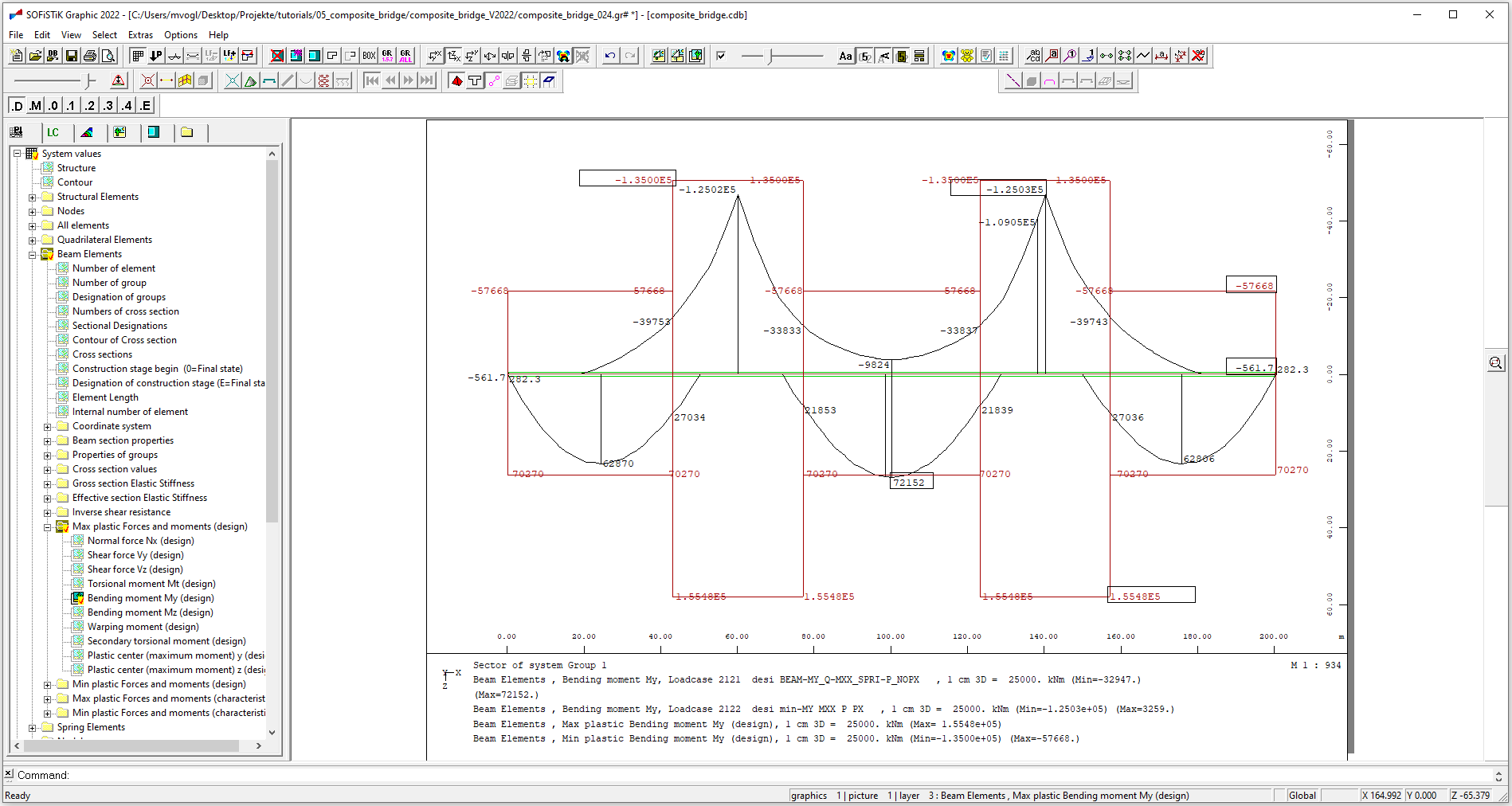
Here we can also check the position of the plastic center (e.g. if it is in the concrete slab) to decide, if a plastic design check would be feasible. If a plastic design check is desired it is possible to contrast the design moments with the plastic design resistance of the cross-sections. This comparison can be plotted using the module “Graphic”:
Linear elastic computation#
To compute the utilisation of each cross-section the command STRE C of module AQB can be used. It can perform the following tasks:
The linear elastic stresses considering construction stages and eigenstresses are computed.
The cross-sections are classified according to EN 1993 based on the calculated linear elastic stresses. For cross-sections classified in class 3 or 4, the steel stresses will be checked against the allowable stress (fEd/
) and the utilisation calculated and saved to the database.
If the section is in class 1 or 2 the utilisation of the cross-section is calculated using the plastic resistance forces and moments and the interaction of forces and moments is calculated according to EN 1993.
Important
The command STRE can not handle the cracking of concrete. How to deal with sections that are defined with an effective concrete part (full elastic modulus), but where the concrete will crack in the design combination is explained in the following section.
Important
For the calculation of shear stresses with the commad STRE the concrete is effective. Especially for composite T-beams a significant part of the shear stresses resulting from torsion can be allocated to the concrete. If it is desired that the torsional moment should only be carried by the steel cross-section, the shear stresses in the structural steel will be underestimated. Be aware that this effect is also valid for cross-sections with a reduced elastic modulus for the concrete. If it is not desired or can not be neglected a computation with the command NSTR (see following section) should be performed. There it can be specified that concrete should not be effective for shear (default setting for composite cross-sections).
Important
For cross-sections classified in class 4 design checks with regard to buckling
(reduction of resistance according to EN 1993-1-5 and check against fy/) are not considered.
These have to be carried out seperately by the user (considering stiffeners if necessary).
Important
Currently the utilisation factor for cross-sections classified in class 3 or 4 is calculated based on the steel stresses, which are in most cases the decisive ones. Concrete stresses are not explicitly checked. This has to be done by the user. We recommend to make use of graphical plots in WING for this purpose.
Note
The classification is carried out only for the steel part of the cross-section. So composite cross-sections where the plastic center is within the concrete slab or the upper flange and which are subjected to a positive design moment (meaning that all structural steel will be in tension for a utilisation of 1.0), will not necessarily be classified in class 1 or 2. If a plastic design check is desired in such cases, we recommend a comparison of design moments and plastic resistance moments as described in the previous section.
You can use this code block:
+PROG AQB $ Linear elastic stress + design checks - ULS
HEAD Linear elastic stress + design checks - ULS
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used
BEAM GRP - CS AUTO
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_D ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3100 LC1 G LC2 C LC3 Y_D 1.0
COMB MIND MY TITL 'ULS_elast_minMY_too' LCST 3101 LC1 G LC2 C LC3 Y_D 1.0
$
COMB MAXD MY TITL 'ULS_elast_maxMY_t1' LCST 3102 LC1 G LC2 C_1 LC3 Y_D 1.0
COMB MIND MY TITL 'ULS_elast_minMY_t1' LCST 3103 LC1 G LC2 C_1 LC3 Y_D 1.0
$
COMB MAXD VZ TITL 'ULS_elast_maxVZ_too' LCST 3104 LC1 G LC2 C LC3 Y_D 1.0
COMB MIND VZ TITL 'ULS_elast_minVZ_too' LCST 3105 LC1 G LC2 C LC3 Y_D 1.0
$
COMB MAXD VZ TITL 'ULS_elast_maxVZ_t1' LCST 3106 LC1 G LC2 C_1 LC3 Y_D 1.0
COMB MIND VZ TITL 'ULS_elast_minVZ_t1' LCST 3107 LC1 G LC2 C_1 LC3 Y_D 1.0
$
COMB MAXD MT TITL 'ULS_elast_maxMT_too' LCST 3108 LC1 G LC2 C LC3 Y_D 1.0
COMB MIND MT TITL 'ULS_elast_minMT_too' LCST 3109 LC1 G LC2 C LC3 Y_D 1.0
$
COMB MAXD MT TITL 'ULS_elast_maxMT_t1' LCST 3110 LC1 G LC2 C_1 LC3 Y_D 1.0
COMB MIND MT TITL 'ULS_elast_minMT_t1' LCST 3111 LC1 G LC2 C_1 LC3 Y_D 1.0
$
COMB GMAX LCST 3112 TITL 'ULS_elast_max'
COMB GMIN LCST 3113 TITL 'ULS_elast_min' $ only for min My,Vz,Mt - max utilisation stored with GMAX
STRE C STYP M0
END
It comprises the following parts:
First we set the control settings. CTRL SVRF assures that the reinforcment is taken into account for creep and shrinkage. With CTRL REIN FIX we explicitly tell the programm not to change the amount of reinforcement. CTRL VRED 0 suppresses the conversion of shear stresses in haunches (conversion should only be used for reinforced or prestressed concrete beams). It is not necessary in this example, because we have no beams with haunches. However we recommed to include this line as standard setting for composite and steel cross-sections.
Next we define which beam elements should be used (BEAM GRP - CS AUTO). Without specifying a group all beam elements are chosen. The setting CS AUTO is important for a correct application of the construction stages.
Furthermore we have to choose the loadcases to be used with the commad LC (all 5XXX and 6XXX loadcases calculated by the “Construction Stage Manager” and the loadcases of type Y_D (combined internal forces from short term loads for ultimate limit state)
With COMB we set the combinations that will be evaluated for the stress calculation resp. the design checks. The meaning of the individual settings are explained for the line:
COMB MAXD MY TITL ‘ULS_design_maxMY_too’ LCST 3100 LC1 G LC2 C LC3 Y_D 1.0
MAXD MY: evaluate the maximum value of the ultimate limit state design combination for the given target force / moment (here: My)
TITL: title of the created result loadcase
LCST: number of the created result loadcase
LC1, LC2, LC3, …: acts / loadcases to be used for the combination (the respective loadcases have to be defined beforehand with LC)
With COMB GMAX / GMIN the maximum / minimum values of the results for the defiined combinations are stored in the given load case. So if we are interestred in the overall maximum von Mises stress and the maximum utilisation level we should for example look at loadcase 3112.
Finally we tell the module AQB to compute the tasks described above with STRE C STYP M0.
Note
As can be seen from the code block above we use two combinations for each moment resp. force, once defined with the action C and the other time with C_1. The combination that uses C (comprising C_1 and C_2) contains all creep and shrinkage loadcases (the state at t_infinity), while the one using C_1 only those until the end of construction (resp. the begin of regular traffic loading). Generally we have to examine these two states seperately, because the loadcases that contain the eigenstresses (6XXX) do not carry information about internal forces. Therefore the COMB command can not decide if the eigenstresses have a positive or negative influence on the results (e.g. the stresses). Also for this reason we have not only defined C_1 but also C_2 as permanent action.
Note
In the current example it is assumed that bending in crossdirection (Mz) and the corresponding forces (Vy) do not play a significant role Therefore we have not included the corresponding combinations MAXD / MIND MZ and MAXD / MIND VY. If necessary they have to be defined analogously to the combinations for MY resp. VZ.
We can display the calculated stresses, the cross-section class and the utilisation factor with “Graphic” for each combination or show the maximum values of the examined combinations stored by GMAX:
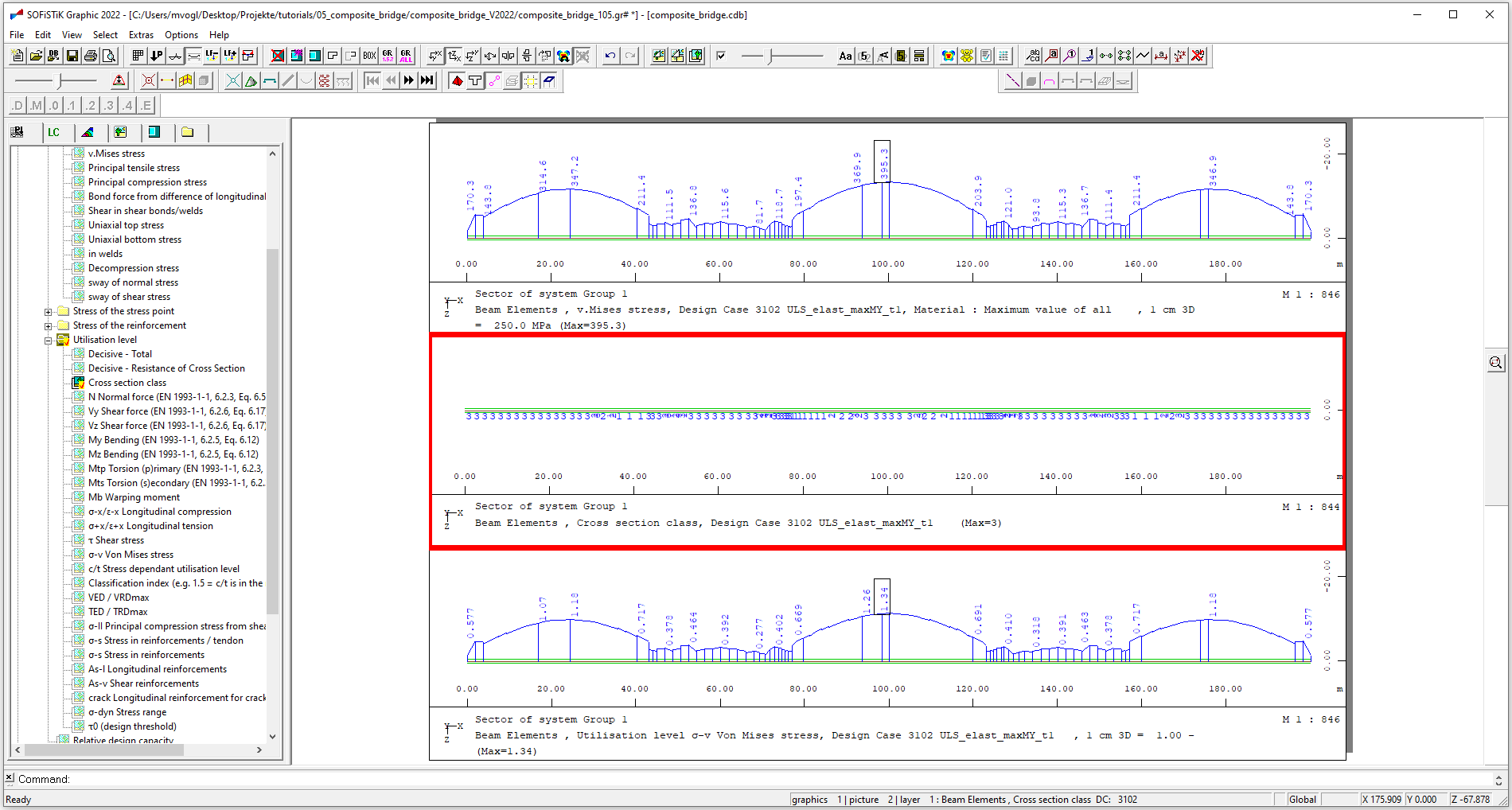
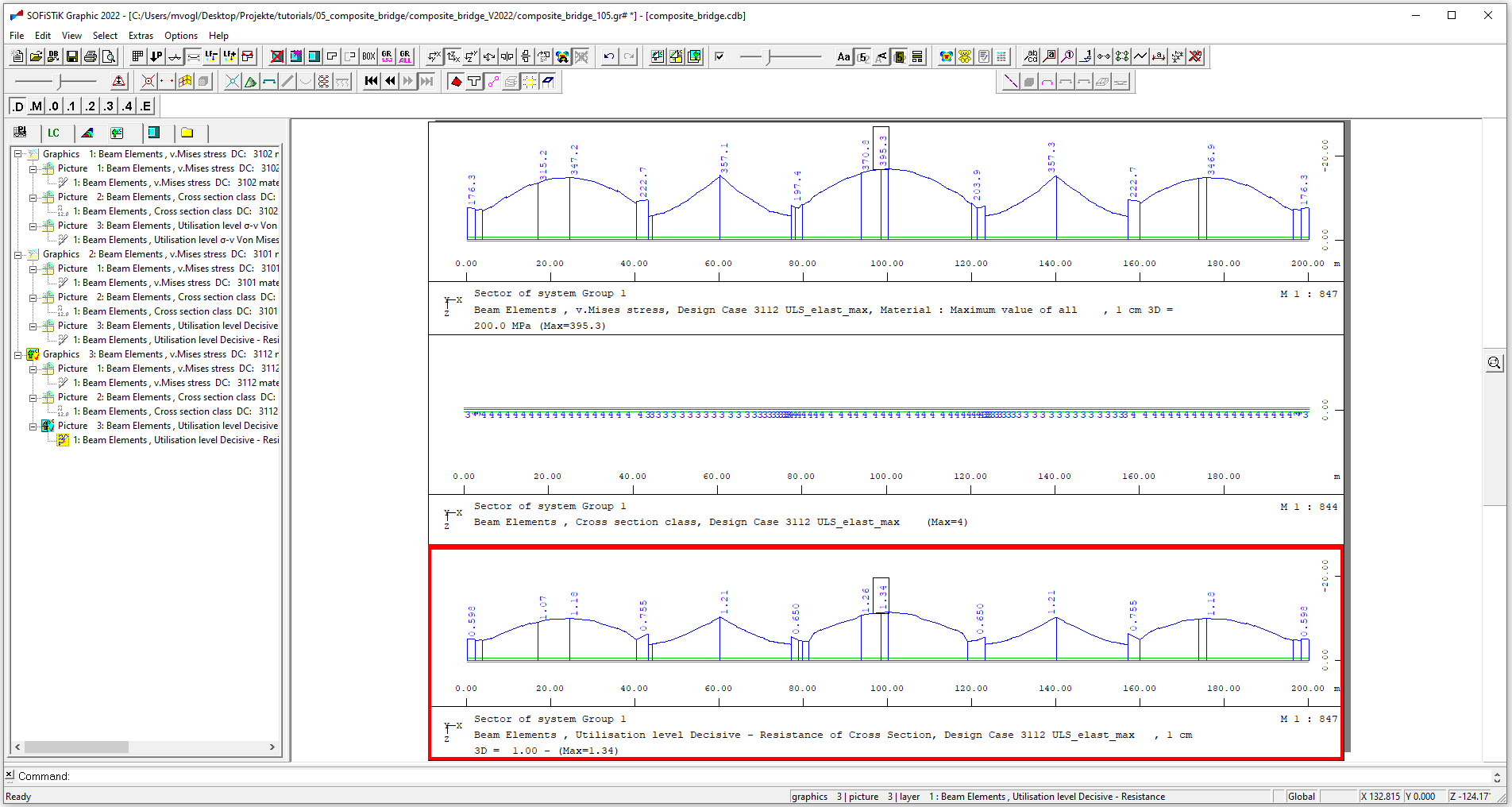
Nonlinear computation (cracked concrete)#
In this tutorial we have composite beams that have been defined using a concrete material with full elastic modulus (material nr. 2 in this tutorial), but where tensional forces occur in the concrete for the design combinations. Here we should calculate the stresses using cross-sectional values for the cracked state (structural steel + reinforcement).
To consider the cracking of concrete we can use the command NSTR of module AQB. To do this create a new “Text Editor” task and insert the following command block (explanation of commands see below):
+PROG AQB $ Nonlinear stress - ULS
HEAD Nonlinear stress - ULS
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_D ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXD MY TITL 'ULS_nonl_maxMY_too' LCST 3200 LC1 G LC2 C LC3 Y_D 1.0
COMB MIND MY TITL 'ULS_nonl_minMY_too' LCST 3201 LC1 G LC2 C LC3 Y_D 1.0
$
COMB MAXD MY TITL 'ULS_nonl_maxMY_t1' LCST 3202 LC1 G LC2 C_1 LC3 Y_D 1.0
COMB MIND MY TITL 'ULS_nonl_minMY_t1' LCST 3203 LC1 G LC2 C_1 LC3 Y_D 1.0
$
COMB MAXD VZ TITL 'ULS_nonl_maxVZ_too' LCST 3204 LC1 G LC2 C LC3 Y_D 1.0
COMB MIND VZ TITL 'ULS_nonl_minVZ_too' LCST 3205 LC1 G LC2 C LC3 Y_D 1.0
$
COMB MAXD VZ TITL 'ULS_nonl_maxVZ_t1' LCST 3206 LC1 G LC2 C_1 LC3 Y_D 1.0
COMB MIND VZ TITL 'ULS_nonl_minVZ_t1' LCST 3207 LC1 G LC2 C_1 LC3 Y_D 1.0
$
COMB MAXD MT TITL 'ULS_nonl_maxMT_too' LCST 3208 LC1 G LC2 C LC3 Y_D 1.0
COMB MIND MT TITL 'ULS_nonl_minMT_too' LCST 3209 LC1 G LC2 C LC3 Y_D 1.0
$
COMB MAXD MT TITL 'ULS_nonl_maxMT_t1' LCST 3210 LC1 G LC2 C_1 LC3 Y_D 1.0
COMB MIND MT TITL 'ULS_nonl_minMT_t1' LCST 3211 LC1 G LC2 C_1 LC3 Y_D 1.0
$
COMB GMAX LCST 3212 TITL 'ULS_nonl_max'
COMB GMIN LCST 3213 TITL 'ULS_nonl_min' $ only for min My,Vz,Mt - max utilisation stored with GMAX
NSTR KSV EL KSB EL
END
The setting of control options, the selection of beams and loadcases and the definition of combinations is done in the same way as in the linear elastic case (see previous section).
Generally with NSTR we can compute strains and stresses using material laws with nonlinear stress-strain-relations (i.e. allowing a plastification of the material)
However in this tutorial we show you how to consider the cracking of concrete, but enforce a linear elastic behavior for the steel. It is done by using NSTR with the setting of KSV EL KSB EL.
Note
For plastic design checks we recommed the procedure described in section “Plastic resistance moments”.
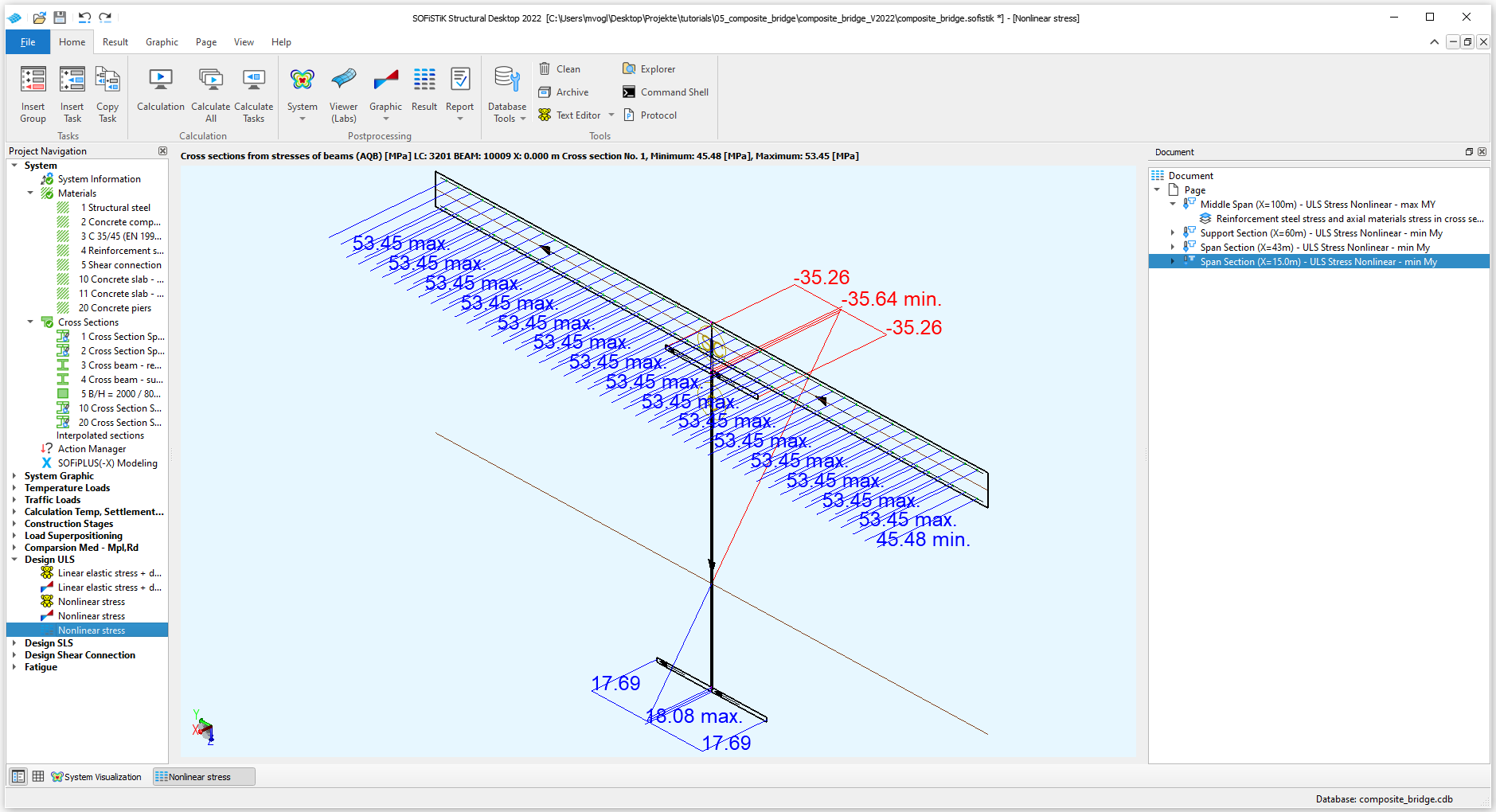
The construction stages and eigenstresses are taken into account for the stress computation with NSTR from SOFiSTiK Version 2020 onwards. To verify this take for example a look at the stresses in the beam element at global X = 15.0 m for a min My combination. As you can see in the “Result Viewer” we have no stress in the concrete (i.e. it is cracked) and tensional forces in the reinforcement. However in the upper flange of the steel profile compressive stresses remain, which have been impressed in the steel profile in construction stage 10 and 19 and are not fully compensated by tensional stresses from short term loads.
Important
Currently nonlinear behavior in construction stages is only supported if the nonlinearity affects only the final cross-section. This is the case in the present example, where the nonlinearity (cracking of the concrete) applies only to the final cross-section (composite section with concrete slab) and the partial cross-section of the earlier construction stages (i.e. the pure structural steel section) remains linear elastic. Be aware that nonlinear behavior in partial cross-sections that are not the final cross-section is currently not supported. Often this is the case for cross-sections where concrete parts are added in more than one construction stages. An example would be precast composite girders with in-situ concrete addition, where cracking of concrete already happens in the precast girder.
Note
In accordance with EN 1994-2 6.2.1.5 (5) eigenstresses due to creep and shrinkage are only taken into account if the section remains uncracked in the examined combination.
Important
If cross-sections are classified in class 4 the non-effective parts according to EN 1993-1-5 are calculated and always taken into account for calculations with NSTR. In this tutorial it is for example the case for the left main beam at global X = 43.0 m for the min My combinations. You can take a look at the visualisation of the stresses in the “Result Viewer” to check out non-effective parts.
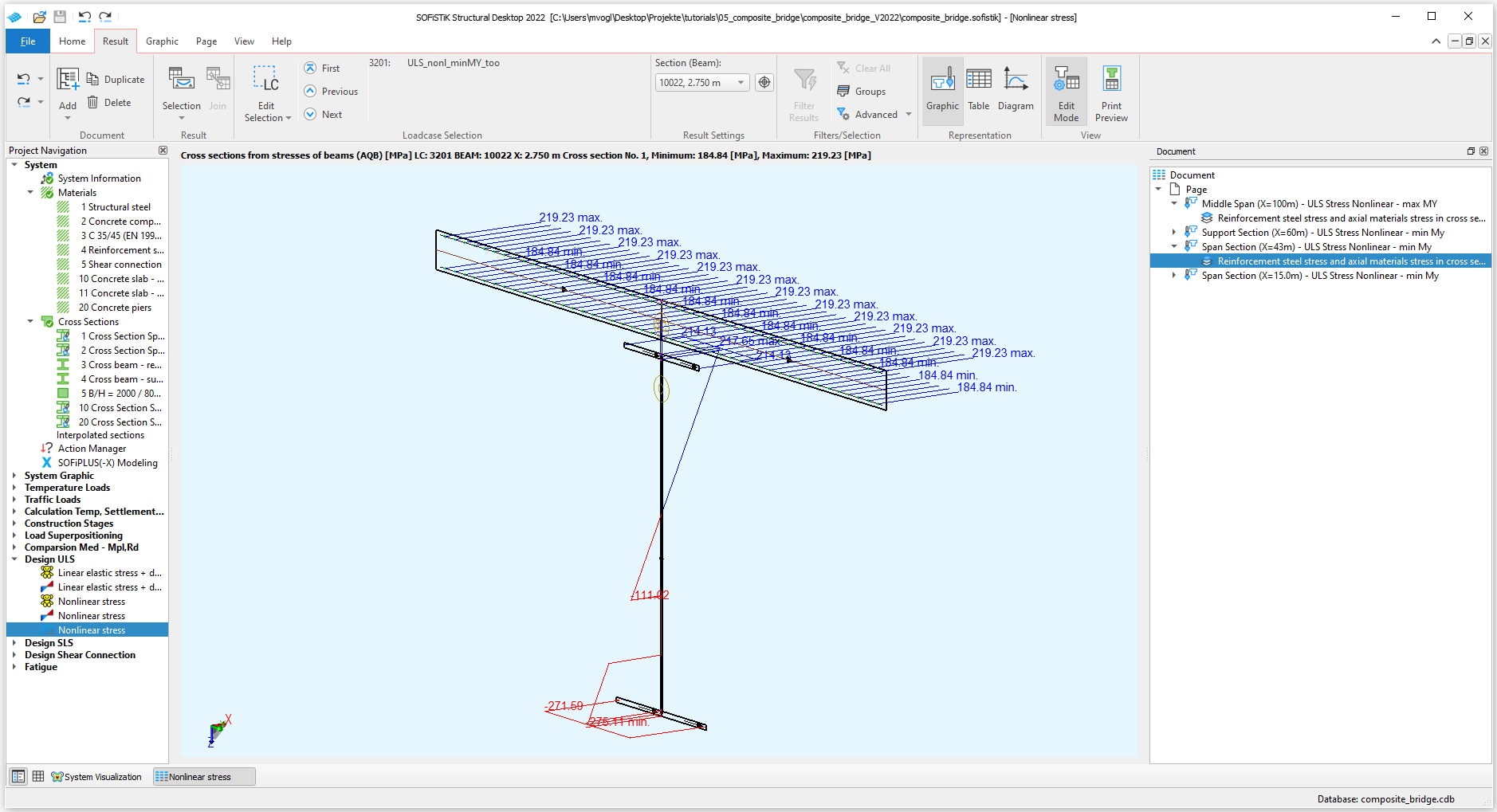
Note
If you use the default setting for composite beams, NSTR assigns torsional moments and shear forces, respectively the resulting shear stresses, only to the structural steel part of the cross-section. In cases where this behavior is not desired, you can add the command CTRL INTE CONC 1 1.0. With this setting the concrete is taken into account for shear with factor 1.0. An example for such a case would be composite box girders modeled with a single cross-section where the concrete part is essential to provide a hollow cross-section for torsion.
Design checks for serviceability limit state#
For the design checks in the serviceability limit state we can use the tools for linear elastic (STRE) and nonlinear (NSTR) stress computation already described above for the ultimate limit state (for their capabilities and limits see there).
In the sequel we will discuss how they can be used for following design checks:
Limitation of structrual steel stresses in the characteristic combination
Limitation of stresses in reinforcement steel in the characteristic combination
Limitation of concrete stresses in the characteristic and permanent combination
Calculation of reinforcement stresses in the frequent combination for crack width checks
Important
The design check against web breathing (DIN EN 1994-2 7.2.3, DIN EN 1993-2 7.4) is not part of the described workflow and has to be checked by the user based on the calculated stresses.
Linear elastic computation#
To carry out a linear elastic stress calculation you can use a “Text Editor” task with the following code block:
+PROG AQB $ Linear elastic stress SLS - rare
HEAD Linear elastic stress SLS - rare
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_1 ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXR MY TITL 'SLS_elast_rare_maxMY_too' LCST 3300 LC1 G LC2 C LC3 Y_1 1.0
COMB MINR MY TITL 'SLS_elast_rare_minMY_too' LCST 3301 LC1 G LC2 C LC3 Y_1 1.0
$
COMB MAXR MY TITL 'SLS_elast_rare_maxMY_t1' LCST 3302 LC1 G LC2 C_1 LC3 Y_1 1.0
COMB MINR MY TITL 'SLS_elast_rare_minMY_t1' LCST 3303 LC1 G LC2 C_1 LC3 Y_1 1.0
$
COMB MAXR VZ TITL 'SLS_elast_rare_maxVZ_too' LCST 3304 LC1 G LC2 C LC3 Y_1 1.0
COMB MINR VZ TITL 'SLS_elast_rare_minVZ_too' LCST 3305 LC1 G LC2 C LC3 Y_1 1.0
$
COMB MAXR VZ TITL 'SLS_elast_rare_maxVZ_t1' LCST 3306 LC1 G LC2 C_1 LC3 Y_1 1.0
COMB MINR VZ TITL 'SLS_elast_rare_minVZ_t1' LCST 3307 LC1 G LC2 C_1 LC3 Y_1 1.0
$
COMB MAXR MT TITL 'SLS_elast_rare_maxMT_too' LCST 3308 LC1 G LC2 C LC3 Y_1 1.0
COMB MINR MT TITL 'SLS_elast_rare_minMT_too' LCST 3309 LC1 G LC2 C LC3 Y_1 1.0
$
COMB MAXR MT TITL 'SLS_elast_rare_maxMT_t1' LCST 3310 LC1 G LC2 C_1 LC3 Y_1 1.0
COMB MINR MT TITL 'SLS_elast_rare_minMT_t1' LCST 3311 LC1 G LC2 C_1 LC3 Y_1 1.0
$
COMB GMAX LCST 3312 TITL 'SLS_elast_rare_max'
COMB GMIN LCST 3313 TITL 'SLS_elast_rare_min' $ only for min My,Vz,mt - max utilisation stored using GMAX
STRE E FF $ linear elastic stress computation and check against full yield strength
END
By using the command STRE E with FF the calculated steel stresses are checked agianst the full yield strength of the material (without safety factor). Now we can for example display the maximum stresses and the utilisation factor stored by GMAX with “Graphic”.
Important
The remarks from section “Linear elastic computation” for the ultimate limit state (not-cracking of concrete, allocation of shear stresses) apply here in the same way.
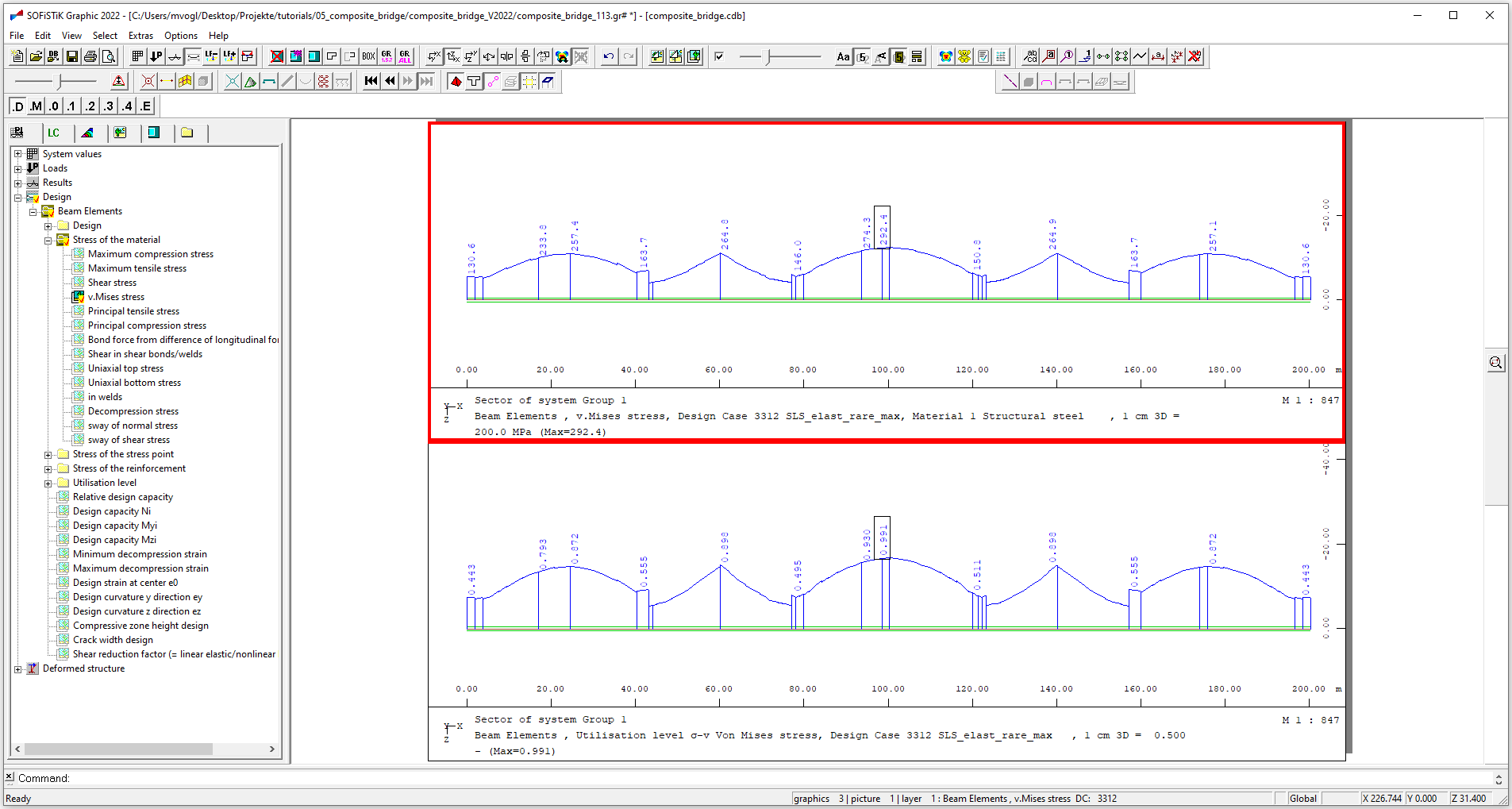
Nonlinear computation (cracked concrete)#
To take the cracking of concrete into account we can use a nonlinear stress computation (see also section “Nonlinear computation” for the ultimate limit state).
Important
A tension stiffening effect for composite beams according to DIN EN 1994-2 7.2.1 (1) is not considered in the stress calculation in this tutorial.
+PROG AQB $ Nonlinear stress SLS - rare
HEAD Nonlinear stress SLS - rare
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_1 ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXR MY TITL 'SLS_nonl_rare_maxMY_too' LCST 3400 LC1 G LC2 C LC3 Y_1 1.0
COMB MINR MY TITL 'SLS_nonl_rare_minMY_too' LCST 3401 LC1 G LC2 C LC3 Y_1 1.0
$
COMB MAXR MY TITL 'SLS_nonl_rare_maxMY_t1' LCST 3402 LC1 G LC2 C_1 LC3 Y_1 1.0
COMB MINR MY TITL 'SLS_nonl_rare_minMY_t1' LCST 3403 LC1 G LC2 C_1 LC3 Y_1 1.0
$
COMB MAXR VZ TITL 'SLS_nonl_rare_maxVZ_too' LCST 3404 LC1 G LC2 C LC3 Y_1 1.0
COMB MINR VZ TITL 'SLS_nonl_rare_minVZ_too' LCST 3405 LC1 G LC2 C LC3 Y_1 1.0
$
COMB MAXR VZ TITL 'SLS_nonl_rare_maxVZ_t1' LCST 3406 LC1 G LC2 C_1 LC3 Y_1 1.0
COMB MINR VZ TITL 'SLS_nonl_rare_minVZ_t1' LCST 3407 LC1 G LC2 C_1 LC3 Y_1 1.0
$
COMB MAXR VZ TITL 'SLS_nonl_rare_maxVZ_too' LCST 3408 LC1 G LC2 C LC3 Y_1 1.0
COMB MINR VZ TITL 'SLS_nonl_rare_minVZ_too' LCST 3409 LC1 G LC2 C LC3 Y_1 1.0
$
COMB MAXR VZ TITL 'SLS_nonl_rare_maxVZ_t1' LCST 3410 LC1 G LC2 C_1 LC3 Y_1 1.0
COMB MINR VZ TITL 'SLS_nonl_rare_minVZ_t1' LCST 3411 LC1 G LC2 C_1 LC3 Y_1 1.0
$
COMB GMAX LCST 3412 TITL 'SLS_nonl_rare_max'
COMB GMIN LCST 3413 TITL 'SLS_nonl_rare_min' $ only for min My,Vz,mt - max utilisation stored using GMAX
NSTR KSV EL KSB EL
END
Plot the calculated stresses with “Graphic”:
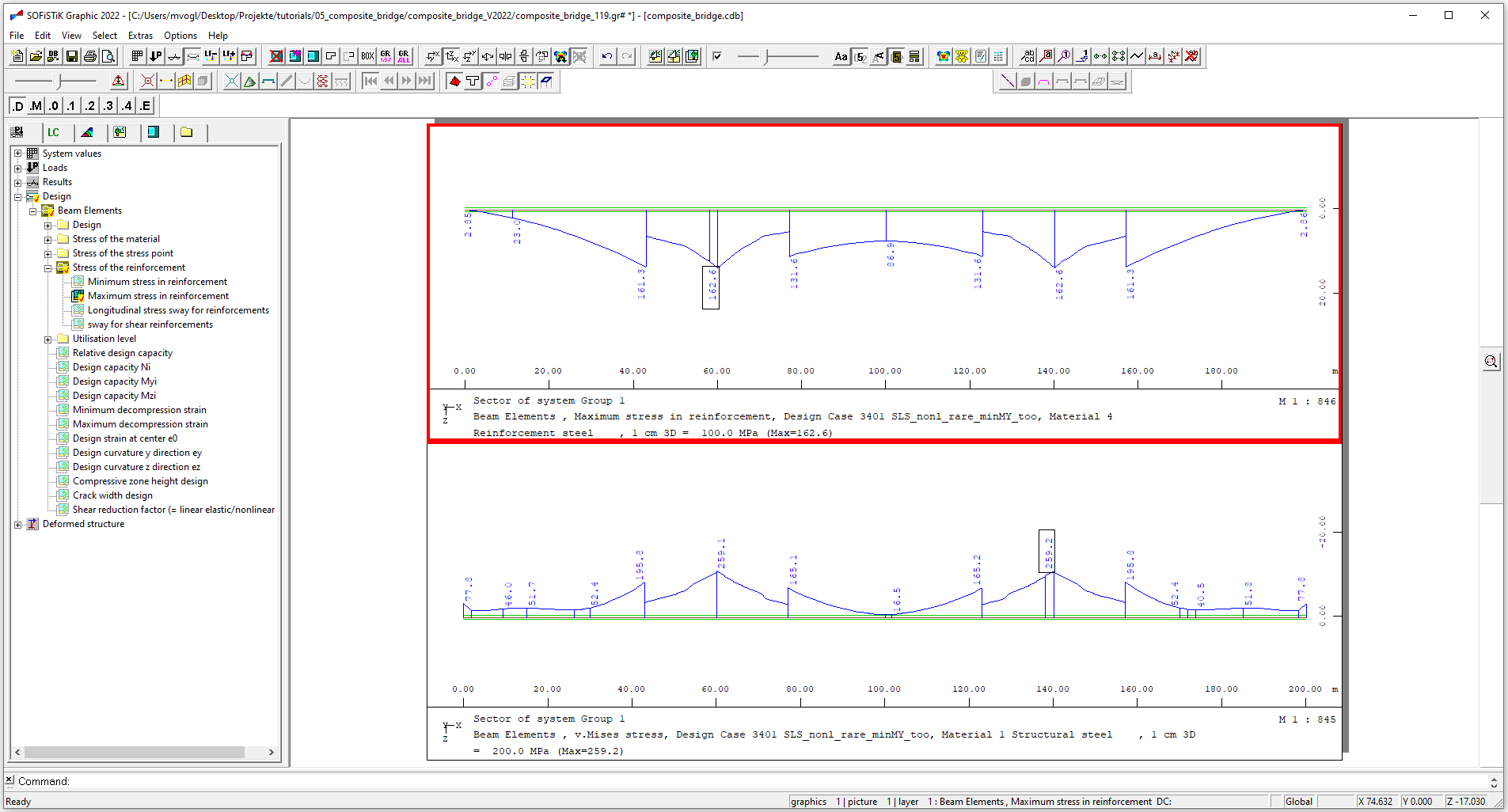
Stress check concrete in characteristic combination#
According to DIN EN 1994-2 7.2.2 (2) and DIN EN 1992-1-1 7.2 (2) the compressive stress in concrete for the characteristic combination should be limited to 0.60 fck. We can check this using module AQB with the command STR E BH:
+PROG AQB $ Stress check concrete SLS - rare
HEAD Stress check concrete SLS - rare
HEAD acc. DIN EN 1994-2:2010 7.2.2(2) resp. DIN EN 1992-1-1 7.2(2)
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_1 ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXR MY TITL 'SLS_rare_concrete_maxMY_too' LCST 3500 LC1 G LC2 C LC3 Y_1 1.0
$COMB MINR MY TITL 'SLS_rare_concrete_minMY_too' LCST 3501 LC1 G LC2 C LC3 Y_1 1.0
$
COMB MAXR MY TITL 'SLS_rare_concrete_maxMY_t1' LCST 3502 LC1 G LC2 C_1 LC3 Y_1 1.0
$COMB MINR MY TITL 'SLS_rare_concrete_minMY_t1' LCST 3503 LC1 G LC2 C_1 LC3 Y_1 1.0
$
COMB GMAX LCST 3504 TITL 'SLS_rare_concrete_max'
$
STRE E BH $ check concrete stress against 0.60 f_ck
END
Note
Only the max My loadcases are activated in the code block, because these are the decisive ones for our example. Combinations for bending in cross-direction (MAXR / MINR MZ) have been omitted as not relevant in the present case.
The utilisation level can be displayed with “Graphic”.
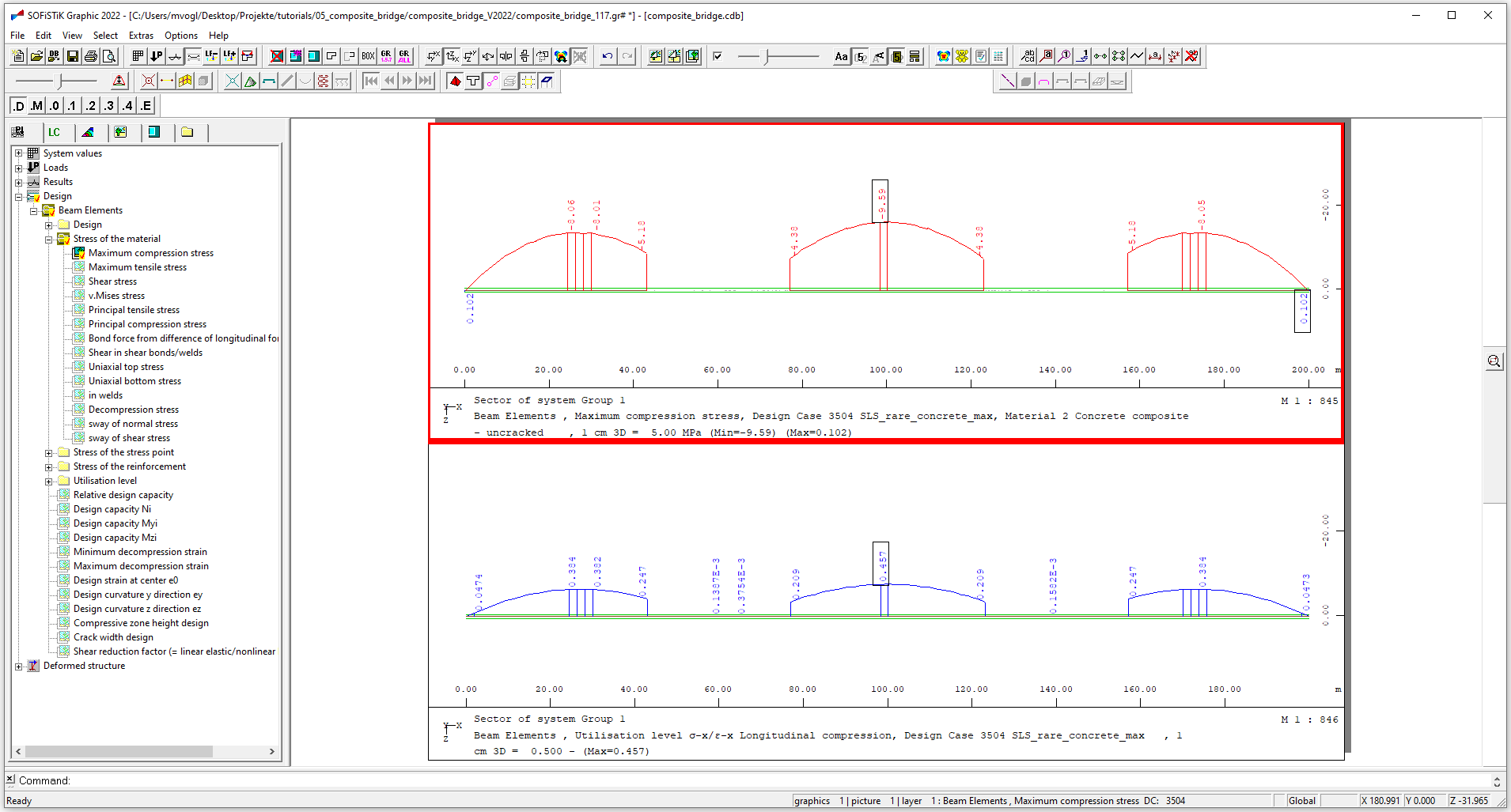
Stress check concrete in permanent combination#
According to DIN EN 1994-2 7.2.2 (2) and DIN EN 1992-1-1 7.2 (3) the compressive stress in concrete for the permanent combination should be limited to 0.45 fck. For this check we can use the module AQB with the command STR E VZ:
+PROG AQB $ Stress check concrete SLS - perm
HEAD Stress check concrete SLS - perm
HEAD acc. DIN EN 1994-2:2010 7.2.2(2) resp. DIN EN 1992-1-1 7.2(3)
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_4 ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXP MY TITL 'SLS_perm_concrete_maxMY_too' LCST 3600 LC1 G LC2 C LC3 Y_4 1.0
$COMB MINP MY TITL 'SLS_perm_concrete_minMY_too' LCST 3601 LC1 G LC2 C LC3 Y_4 1.0
$
COMB MAXP MY TITL 'SLS_perm_concrete_maxMY_t1' LCST 3602 LC1 G LC2 C_1 LC3 Y_4 1.0
$COMB MINP MY TITL 'SLS_perm_concrete_minMY_t1' LCST 3603 LC1 G LC2 C_1 LC3 Y_4 1.0
$
COMB GMAX LCST 3604 TITL 'SLS_perm_concrete_max'
STRE E VZ $ check concrete stress against 0.45 f_ck
END
Note
Only the max My loadcases are activated in the code block, because these are the decisive ones for our example. Combinations for bending in cross-direction (MAXR / MINR MZ) have been omitted as not relevant in the present case.
As for the characteristic combination you can display the utilisation with “Graphic”.
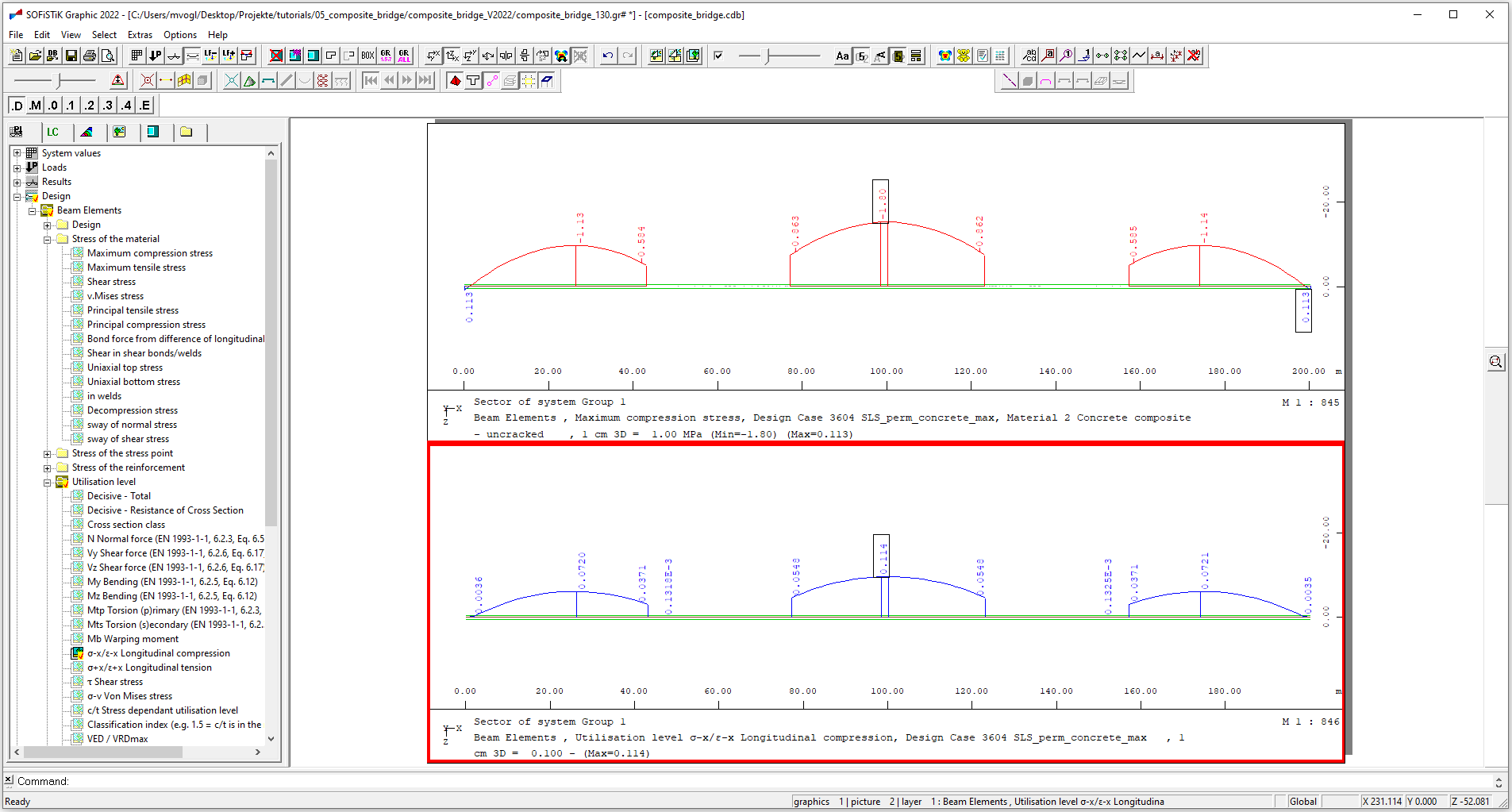
Reinforcement stress for crack width checks#
Two apects have to be checked for the limitation of the crack width in the concrete slab:
the minimum reinforcement (DIN EN 1994-2 7.4.2), mainly depending on the geometry and material properties of the concrete slab
the control of the crack width due to direct loading (DIN EN 1994-2 7.4.3), mainly depending on the reinforcement stress (in the standard case evaluated for the frequent combination)
For composite beams we currently do not provide tools to calculate the necessary amount of minimum reinforcement.
For the check of the crack width due to direct loading we can compute the reinforcement stress in the frequent combination using following code block:
+PROG AQB $ Reinforcement stress SLS - freq (crack width)
HEAD Reinforcement stress SLS - freq (crack width)
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_3 ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
$COMB MAXF MY TITL 'SLS_nonl_freq_maxMY_too' LCST 3700 LC1 G LC2 C LC3 Y_3 1.0
COMB MINF MY TITL 'SLS_nonl_freq_minMY_too' LCST 3701 LC1 G LC2 C LC3 Y_3 1.0
$
$COMB MAXF MY TITL 'SLS_nonl_freq_maxMY_t1' LCST 3702 LC1 G LC2 C_1 LC3 Y_3 1.0
COMB MINF MY TITL 'SLS_nonl_freq_minMY_t1' LCST 3703 LC1 G LC2 C_1 LC3 Y_3 1.0
$
COMB GMAX LCST 3704 TITL 'SLS_nonl_freq_max'
NSTR KSV EL KSB EL
END
Note
Only the min My loadcases are activated in the code block, because these are the decisive ones for our example. Combinations for bending in cross-direction (MAXR / MINR MZ) have been omitted as not relevant in the present case.
Important
A tension stiffening effect for composite beams according to DIN EN 1994-2 7.4.1 (2) is not considered in the stress calculation in this tutorial. To take it into account we recommed an increase of the computed reinforcement stress using the procedure given in DIN EN 1994-2 7.4.3 (3). The check of the crack width can then for example be carried out using DIN EN 1994-2 table 7.1.
Important
Thermal shrinkage of the concrete slab due to heating effects from the hydration of cement (see DIN EN 1994-2 7.4.1 (6)) is not considered in this example. It has been assumed that measures are taken during construction to limit these effects.
Calculation of bond forces#
In this section we show you how to calculate the bond forces between concrete and structural steel for the design of shear connectors. According to DIN EN 1994-2 6.6.2.1(2) in general the elastic properties of the uncracked section should be used for the determination of the longitudinal shear force. To consider the cracking of concrete in the global analysis we have used the cracked flexural stiffness at the inner supports. For this purpose we have reduced the elastic modulus of the concrete in this regions. To use the uncracked cross-sectional values for the calculation of the shear forces we have to set back the material properties of the concrete temporarily. Then we perform the design check and change back the materials to the cracked condition for consistency reasons.
According to DIN EN 1994-2 6.8.1(3) and DIN EN 1994-2 7.2.2(6) we should also check if the shear force in the characteristic combination in the headed stud connectors does not exceed a certain percentage of their design resistance (ks x PRd). Therefore we perform a AQB-run for the ULS and a second one for the characteristic combination.
+PROG AQUA
HEAD Change Material Properties
ECHO FULL NO
ECHO MAT YES
CTRL REST 3
CONC 3 C 35 TITL 'Concrete composite - UNcracked' $ original material properties - uncracked
END
+PROG AQB $ Calculate Bond Force - Combination ULS
HEAD Calculate Bond Force - Combination ULS
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases / actions to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
LC TYPE 'Y_D ' CST 9998 REF GROS $ pre superposed container without GPC
$ combinations:
COMB EXTR MAXD SCOM VZ LC1 G LC2 C LC3 Y_D LCST 3800 TITL 'Bondforce uncr - MAXD VZ too'
COMB EXTR MIND SCOM VZ LC1 G LC2 C LC3 Y_D LCST 3801 TITL 'Bondforce uncr - MIND VZ too'
COMB EXTR MAXD SCOM VZ LC1 G LC2 C_1 LC3 Y_D LCST 3802 TITL 'Bondforce uncr - MAXD VZ t1'
COMB EXTR MIND SCOM VZ LC1 G LC2 C_1 LC3 Y_D LCST 3803 TITL 'Bondforce uncr - MIND VZ t1'
COMB GMAX LCST 3804 TITL 'Bondforce uncr - ULS'
STRE E
END
+PROG AQB $ Calculate Bond Force - Combination RARE
HEAD Calculate Bond Force - Combination RARE
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases / actions to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
LC TYPE 'Y_1 ' CST 9998 REF GROS $ pre superposed container without GPC
$ combinations:
COMB EXTR MAXR VZ LC1 G LC2 C LC3 Y_1 LCST 3810 TITL 'Bondforce uncr - MAXR VZ too'
COMB EXTR MINR VZ LC1 G LC2 C LC3 Y_1 LCST 3811 TITL 'Bondforce uncr - MINR VZ too'
COMB EXTR MAXR VZ LC1 G LC2 C_1 LC3 Y_1 LCST 3812 TITL 'Bondforce uncr - MAXR VZ t1'
COMB EXTR MINR VZ LC1 G LC2 C_1 LC3 Y_1 LCST 3813 TITL 'Bondforce uncr - MINR VZ t1'
COMB GMAX LCST 3814 TITL 'Bondforce uncr - SLS RARE'
STRE E
END
+PROG AQUA urs:47.4
HEAD Change back Material Properties
ECHO FULL NO
ECHO MAT YES
CTRL REST 3
CONC 3 C 35 EC 300 GMOD 14199 TITL 'Concrete Composite - cracked' $ material properties cracked as defined in task "Materials"
END
You can display the maximum bond forces stored by GMAX with “Graphic” (make sure to choose the material of the shear connection in the “LC” tab):
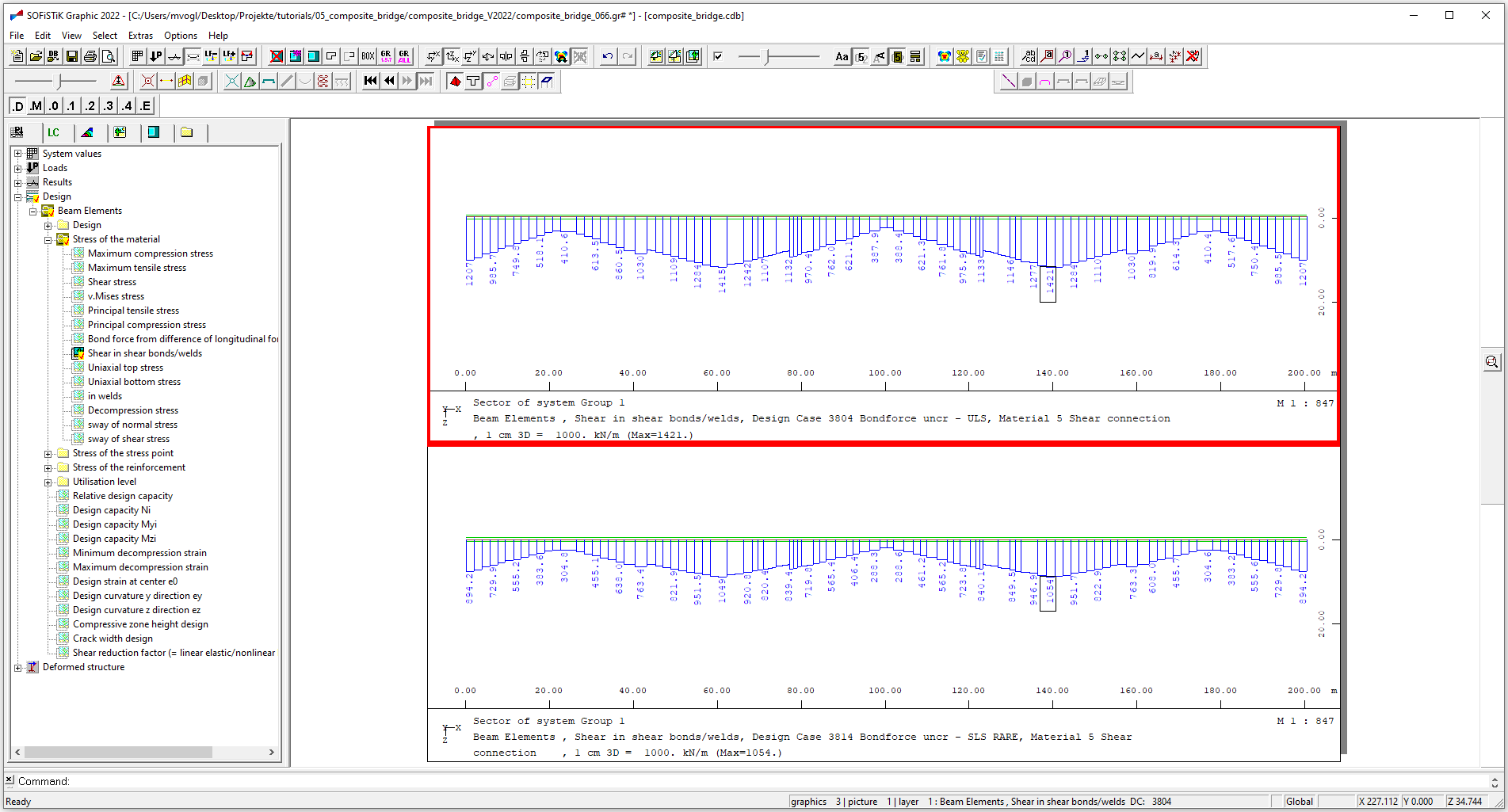
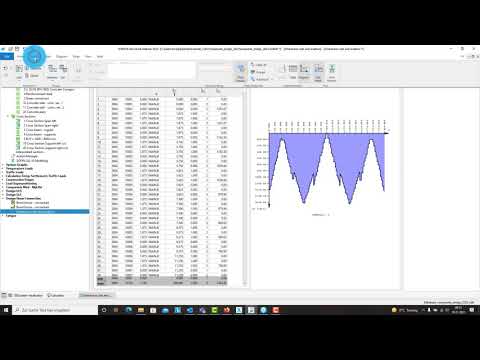
For postprocessing you can create diagrams and tables in the “Result Viewer” and export them as shown in the following video.
Note
Local effects of concentrated longitudinal shear forces according to EN 1994-2 6.6.2.3 and 6.6.2.4 are not considered by the program.
Stress sway calculation for fatigue design checks#
Fatigue load model FLM3 (Definition and Linear Analysis)#
First create the additional action “FAT” for the traffic load model for fatigue.
The axle loads of the fatigue load model FLM3 can be defined with the Load Stepping Method in the same way as the regular TS traffic loads. The main difference is that we use load train “FLM3” in the following code block instead of “LM1”.
+PROG SOFILOAD $ Define lane
HEAD Define lane
LANE MAIN TYPE EN WL -5.50 WR 5.50 YLA -6.00 YRA 6.00 $$ $ define lane
SA 0.00 SE 60.00 $ define span 1
SA 60.00 SE 140.00 $ define span 2
SA 140.00 SE 200.00 $ define span 3
END
+PROG SOFILOAD $ Load trains and traffic toads
HEAD Load train FLM3
ECHO LOAD EXTR
$ Define Load Train FLM3
LC 110 TYPE NONE
TRAI FLM3
$ Loadstepping FLM3
LET#DX 5
LET#X 0
LOOP#I 41
LC 400+#I TYPE L_F ; COPY 110 REF 'MAIN.20' DX #X WIDE 1 type gr0 $ lane with FLM3 positioned at "left" lane
LET#X #X+#DX
ENDLOOP
END
After the definition of the fatigue loads you can carry out a linear analysis. Keep in mind to reduce the stiffness of the QUAD-elements in longitudinal direction with QUEA and QUEMX.
+PROG ASE urs:13.1 $ Linear Analysis
HEAD Calculation of forces and moments
PAGE UNII 0
CTRL OPT WARP VAL 0
CTRL OPT SPRI VAL 12
GRP2 NO 20,30 QUEA 0.01 QEMX 0.01 $ Reduce the QUAD-stiffness in longitudinal direction
LC (400 440 1)
END
Calculation of stress sway#
For the computation of the stress sway the possible cracking of the concrete has to be considered. This can be done by using a nonlinear stress computation with the NSTR command of AQB (as already shown in the sections for ULS and SLS design).
According to EN 1994-2 6.8.4(1) the calculation of forces and moments should be carried out considering non-cycling and fatigue-inducing cyclic actions as given in EN 1992-1-1 6.8.3.
The concept is to have a base combination of the non-cycling actions (the decisive frequent combination of permanent loads, temperature loads and settlements) on which then the fatigue-inducing cyclic action (e.g. fatigue load model FLM3) is superposed.
If we have carried out the load superpositioning with CSM DESI as shown in this tutorial, then presuperposed envelopes for temperature and settlements in the frequent combination are determined. These are saved in the loadcases 1841 - 1852 and can be used to define base combinations.
Note
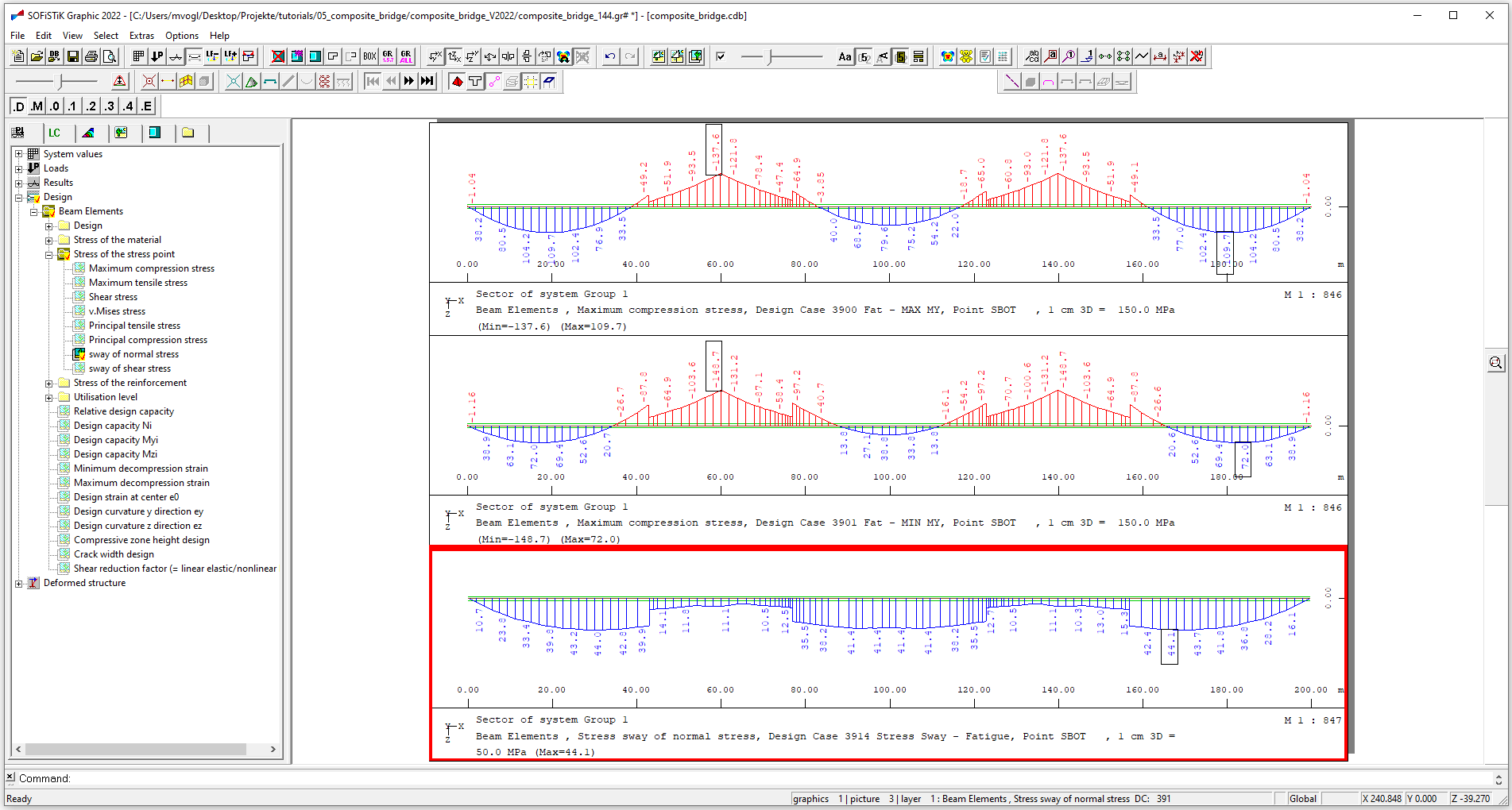
In this tutorial we investigate only the base combination for min My, because for the present system this leads to tension resp. cracking in the concrete slab in the widest areas and consequently to the decisive stress sways.
You can use the following text block for the computation of stress sways:
+PROG AQB $ Calculate Stress Sway - Fatigue
HEAD Calculate Stress Sway - Fatigue
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used:
BEAM GRP - CS auto
$ loadcases / actions to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
LC TYPE 'FAT' CST 9998 REF GROS
LC 1842 CST 9998 REF GROS $ Temp + Settlement frequent
$ min My usually decisive for max delta sigma for standard composite sections
$ combinations:
COMB EXTR MAXF MY LC1 G LC2 C LC3 1842 LC4 FAT LCST 3900 TITL 'Fat - MAX MY'
COMB EXTR MINF MY LC1 G LC2 C LC3 1842 LC4 FAT LCST 3901 TITL 'Fat - MIN MY'
COMB EXTR MAXF VZ LC1 G LC2 C LC3 1842 LC4 FAT LCST 3902 TITL 'Fat - MAX VZ'
COMB EXTR MINF VZ LC1 G LC2 C LC3 1842 LC4 FAT LCST 3903 TITL 'Fat - MIN VZ'
COMB GMAX LCST 3914 TITL 'Stress Sway - Fatigue'
NSTR KSV EL KSB EL FAT EN92
END
In the part where the combinations are defined (COMB … ) you can see the base combination defined by “LC1 G LC2 C LC3 1842”. The loadcase 1842 comprises the frequent min My combination of temperature loads and settlements.
To evaluate stress sways it is necessary to add “FAT EN92” to the “NSTR” command. Then the difference of maximum and minimum stresses of the evaluated loadcases will be calculated for each stress point and saved in the loadcase given by COMB GMAX. Prerequisit for this workflow is that stress points have been defined in the cross-section at the position of the construction details to be investigated.
Note
In this tutorial we only investigate the combinations for min/max My and Vz, as these are the decisive ones in the present case. Depending on the system it may be necessary to include additional combinations for Mt, Mz and Vy.
Important
This workflow gives the pure stress range caused by the fatigue loads.
Damage equivalent factors () have to be considered by the user in the design checks.
Important
Tension stiffening is not considered in the stress calculations in this tutorial, if necessary it has to be considered by the user seperately.
You can depict the maximum and minimum stresses and the stress sway for example as shown below.
Notes on axis based reinforcement definition#
If you have varying amounts of reinforcements along the bridge axis and you do not want to define an individual master cross-section for each reinforcement change you have following alternative possibilities for the reinforcement definition (There is also an example file, composite_bridge_reinforc_along_axis_2022, showing this concepts in the download folder).
Reinforcement definition along axis.
As first step you define a minimum reinforcement in the cross-section just as shown in the video in the chapter “System definition in SOFiPLUS”.
The actual amount of reinforcement along the axis can then be specified in the following way.
Create a user task and insert a text block similar to the following example.
+PROG AQB
HEAD Reinforcement along axis
<TEXT> Explanation
With this input a reinforcement distribution for AQB is defined with the BEAM command and the setting CS AS.
This is done for all beam elements related to the axis specified with REF '...'.
The amount of reinforcement is defined in cm^2 in a section between X and XE.
The reinforcement can be specified for different reinforcement layers.
For layer 1 you have to set CS1 and then the amount of reinforcement.
For layer 2 CS2 ... and so on.
</TEXT>
ECHO FULL FULL
REIN SECT RMOD SAVE $ save as global minimum reinforcement
!*!Label Layer M1
BEAM REF 'MAIN' X 0 XE 43 CS AS CS1 90[cm2]
BEAM REF 'MAIN' X 43 XE 77 CS AS CS1 90[cm2]
BEAM REF 'MAIN' X 77 XE 123 CS AS CS1 90[cm2]
BEAM REF 'MAIN' X 123 XE 157 CS AS CS1 90[cm2]
BEAM REF 'MAIN' X 157 XE 200 CS AS CS1 90[cm2]
!*!Label Layer M2
BEAM REF 'MAIN' X 0 XE 43 CS AS CS2 90[cm2]
BEAM REF 'MAIN' X 43 XE 77 CS AS CS2 140[cm2]
BEAM REF 'MAIN' X 77 XE 123 CS AS CS2 90[cm2]
BEAM REF 'MAIN' X 123 XE 157 CS AS CS2 140[cm2]
BEAM REF 'MAIN' X 157 XE 200 CS AS CS2 90[cm2]
END
We recommend to do this kind of reinforcement definition directly after the import of the system from SOFiPLUS. In this way the reinforcement will be considered in all the following AQB tasks. You should however be aware, that the reinforcement defined in this way is NOT considered in the cross-sectional values in AQUA and the corresponding AQUA-report. Therefore it is also not taken into account for the stiffness of the beam elements in the linear analysis tasks.
With the workflow above you will define the same reinforcement for both main beams.
If you want to define different reinforcements for the main beams you can do it alternatively like this
First create one “dummy” structural line without cross-section along the position of each main beam.
It is important to create this line with the setting “segment on axis”.
Create the line in one segment, then extend the line, so that it reaches over the complete length of the bridge.
You can do this by clicking on an end point of the line and then clicking on the position where you want to drop this point.
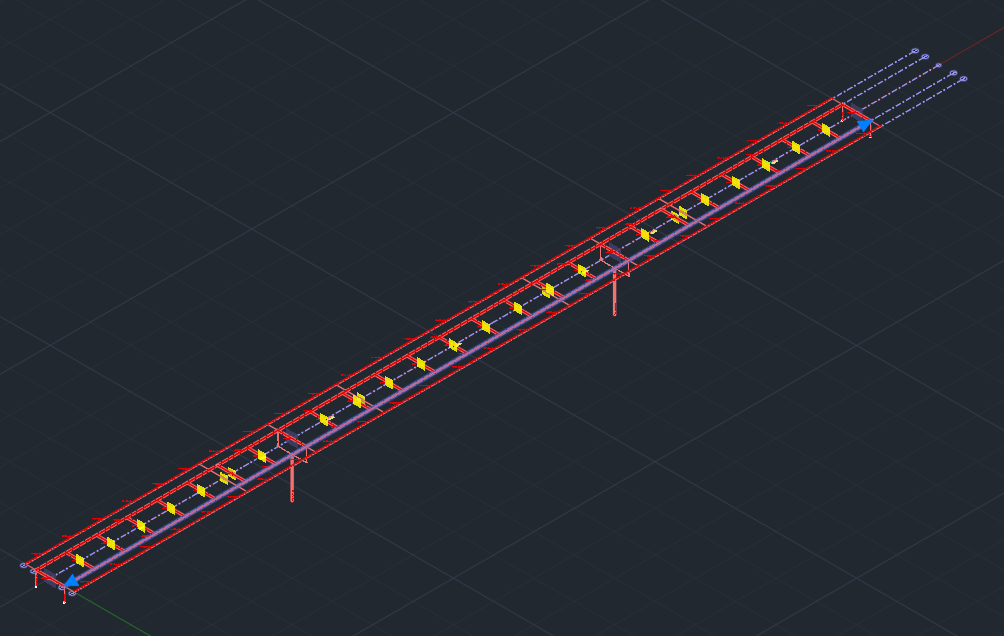
You can then reference this structural line quite in the same way as shown above for the axis. The corresponding input can for example look like this
+PROG AQB
HEAD Reinforcement along structural line
<TEXT> Explanation
With this input a reinforcement distribution for AQB is defined with the BEAM command and the setting CS AS.
This is done for a "dummy" structural line given by SLN ...
The specified reinforcement applies to the beams in the position of that structural line.
The amount of reinforcement is defined in cm^2 in a section between X and XE.
The reinforcement can be specified for different reinforcement layers.
For layer 1 you have to set CS1 and then the amount of reinforcement.
For layer 2 CS2 ... and so on.
</TEXT>
ECHO FULL EXTR
REIN SECT RMOD SAVE $ save as global minimum reinforcement
!*!Label Layer M1
$ Left main beam (-> dummy sln 201)
beam SLN 201 x 0 xe 43 CS AS CS1 80[cm2]
beam SLN 201 x 43 xe 77 CS AS CS1 80[cm2]
beam SLN 201 x 77 xe 123 CS AS CS1 80[cm2]
beam SLN 201 x 123 xe 157 CS AS CS1 80[cm2]
beam SLN 201 x 157 xe 200 CS AS CS1 80[cm2]
$ Right main beam (-> dummy sln 202)
beam SLN 202 x 0 xe 43 CS AS CS1 100[cm2]
beam SLN 202 x 43 xe 77 CS AS CS1 100[cm2]
beam SLN 202 x 77 xe 123 CS AS CS1 100[cm2]
beam SLN 202 x 123 xe 157 CS AS CS1 100[cm2]
beam SLN 202 x 157 xe 200 CS AS CS1 100[cm2]
!*!Label Layer M2
$ Left main beam (-> dummy sln 201)
beam SLN 201 x 0 xe 43 CS AS CS2 80[cm2]
beam SLN 201 x 43 xe 77 CS AS CS2 130[cm2]
beam SLN 201 x 77 xe 123 CS AS CS2 80[cm2]
beam SLN 201 x 123 xe 157 CS AS CS2 130[cm2]
beam SLN 201 x 157 xe 200 CS AS CS2 80[cm2]
$ Right main beam (-> dummy sln 202)
beam SLN 202 x 0 xe 43 CS AS CS2 100[cm2]
beam SLN 202 x 43 xe 77 CS AS CS2 150[cm2]
beam SLN 202 x 77 xe 123 CS AS CS2 100[cm2]
beam SLN 202 x 123 xe 157 CS AS CS2 150[cm2]
beam SLN 202 x 157 xe 200 CS AS CS2 100[cm2]
end