Nonlinear temperature#
Introduction#
If you want to model the temperature difference according to EN 1991-1-5 6.1.4.2 (approach 2) it is possible to create loads with nonlinear temperature gradients.
On this page we show this possibility for the simplified approach for composite bridges with a temperature difference of the concrete slab of +/- 10°C vis-a-vis the structural steel section.
To define temperature loads of this kind create a “User Task” with the following code block:
+PROG SOFILOAD
HEAD Nonlinear temperature loads
LC 83 TYPE NONE TITL 'dTM+'
BEAM GRP 1,2 TYPE T EZA 0 PA 10 REFT -Z
BEAM GRP 1,2 TYPE T EZA 308 PA 10 REFT -Z
BEAM GRP 1,2 TYPE T EZA 309 PA 0 REFT -Z
BEAM GRP 1,2 TYPE T EZA 3217 PA 0 REFT -Z
EVAL TYPE TEIG
LC 84 TYPE NONE TITL 'dTM-'
BEAM GRP 1,2 TYPE T EZA 0 PA -10 REFT -Z
BEAM GRP 1,2 TYPE T EZA 308 PA -10 REFT -Z
BEAM GRP 1,2 TYPE T EZA 309 PA 0 REFT -Z
BEAM GRP 1,2 TYPE T EZA 3217 PA 0 REFT -Z
EVAL TYPE TEIG
END
It is important to define the temperature over the whole cross-section. The lines specifying the structural steel temperature as 0°C should not be neglected!
Be aware that for thin walled cross-sections the procedure is only implemented for constant temperature values within each thin walled element (as is the case in our example where we have constant values within the structural steel part (0°C) and the concrete slab (+10°C resp. -10°C)). Note that the procedure is also not yet implemented for cross-sections with non-effective areas (NEFFs).
A nonlinear temperature distribution can be decomposed in an equivalent uniform temperature change, an equivalent temperature difference in local z and a remaining nonlinear part as shown in the following figure.
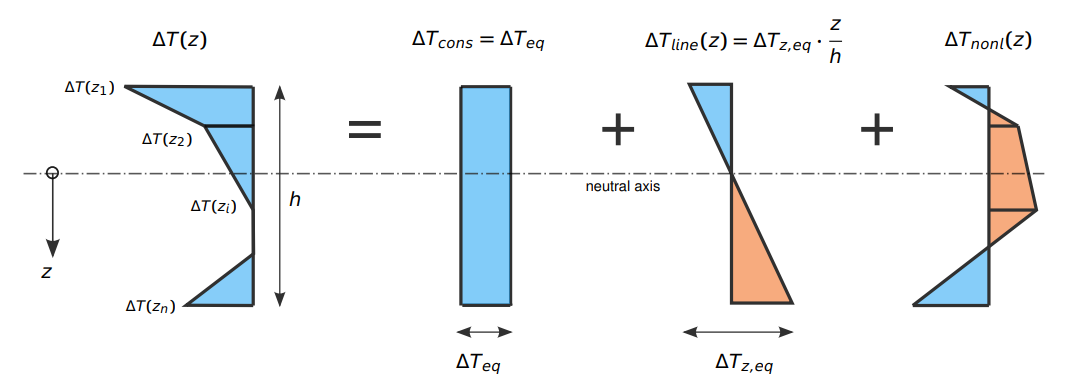
The uniform temperature change and the temperature difference lead to deformations and in statically indeterminate systems also to forces and stresses. The remaining nonlinear part is related to eigenstresses in the cross-section. With the command EVAL TYPE TEIG these components of the overall nonlinear temperature distribution are calculated and saved for further analysis (for more details see the explanations for the command EVAL in the manual of module SOFILOAD).
Combination of Temperature Loads#
You can also combine the nonlinear temperature loads with uniform temperature changes (acc. EN 1991-1-5 6.1.5). Note that it is important to add EVAL TYPE TEIG if you use loadcases with nonlinear temperature gradients.
+PROG SOFILOAD
HEAD Temperature Load Combinations
$ Load combinations
LC 91 TYPE T TITL 'T summer posdt TN+wm*dT' ; COPY 81 ; COPY 83 FACT 0.75 ; EVAL TYPE TEIG
LC 92 TYPE T TITL 'T summer negdt TN+wm*dT' ; COPY 81 ; COPY 84 FACT 0.75 ; EVAL TYPE TEIG
LC 93 TYPE T TITL 'T winter posdt TN+wm*dT' ; COPY 82 ; COPY 83 FACT 0.75 ; EVAL TYPE TEIG
LC 94 TYPE T TITL 'T winter negdt TN+wm*dT' ; COPY 82 ; COPY 84 FACT 0.75 ; EVAL TYPE TEIG
LC 95 TYPE T TITL 'T summer posdt wn*TN+dT' ; COPY 81 FACT 0.35 ; COPY 83 ; EVAL TYPE TEIG
LC 96 TYPE T TITL 'T summer negdt wn*TN+dT' ; COPY 81 FACT 0.35 ; COPY 84 ; EVAL TYPE TEIG
LC 97 TYPE T TITL 'T winter posdt wn*TN+dT' ; COPY 82 FACT 0.35 ; COPY 83 ; EVAL TYPE TEIG
LC 98 TYPE T TITL 'T winter negdt wn*TN+dT' ; COPY 82 FACT 0.35 ; COPY 84 ; EVAL TYPE TEIG
END
Further notes#
In the standard design workflow the superpositioning for the design combinations is done by the task “CSM Bridge Design - Superpositioning”. The live loads are presuperposed and stored in load containers (Y_D, Y_1, etc.), which are then used for the calculation of stresses with the module AQB. However the superpositioning of the live loads is only based on forces, and only the superposed internal forces are stored in the load containers and used for the stress calculation. Eigenstresses from the remaining nonlinear part of the temperature loadcases are lost in this approach.
To take into account these eigenstresses it is necessary to use the temperature loadcases directly in the stress calculation in module AQB.
This makes the superposition and stress calculation tasks more complex. Therefore we recommed to asses the influence of the eigenstresses due to the remaining nonlinear temperature gradient on a simple system or by hand calculation and check if it has a relevant influence in comparison with the overall stresses.
If temperature is not the leading action in the overall design combination you can also use following procedure:
Use the task “CSM Bridge Design - Superpositioning” without temperature loads (action T).
Add the temperature loads directly in the combinations in module AQB. Then the AQB tasks will look like this (here only shown for the combination MAXD MY and STRE C, to be extended for other relevant combinations / design checks):
+PROG AQB urs:32.1 $ Linear elastic stress + design checks - ULS
HEAD Linear elastic stress + design checks - ULS
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement for C+S
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used
BEAM GRP - CS AUTO
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
LC TYPE 'T'
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_D ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3100 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 91 F4 1.35*0.6
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3101 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 92 F4 1.35*0.6
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3102 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 93 F4 1.35*0.6
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3103 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 94 F4 1.35*0.6
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3104 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 95 F4 1.35*0.6
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3105 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 96 F4 1.35*0.6
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3106 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 97 F4 1.35*0.6
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3107 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 98 F4 1.35*0.6
$
COMB GMAX LCST 3112 TITL 'ULS_elast_max'
COMB GMIN LCST 3113 TITL 'ULS_elast_min'
STRE C STYP M0
END
Because of the eigenstresses the decision which temperature loadcase is the most unfavourable can not be based on the internal forces. Consequently every temperature loadcase has to be investigated in an extra combination (in the general case). Note that the factor for the temperature loadcases is set explicitly (gamu*psi0).
A simplification can be made under the assumption that the selection of the decisive temperature loadcase can be based on the internal forces.
+PROG AQB urs:32.1 $ Linear elastic stress + design checks - ULS
HEAD Linear elastic stress + design checks - ULS
ECHO FULL FULL
$ control settings:
CTRL SVRF 1.00000 $ take into account reinforcement for C+S
CTRL REIN FIX $ do not change reinforcement
CTRL VRED 0 $ no conversion of shear forces in haunches
$ beams to be used
BEAM GRP - CS AUTO
$ loadcases to be used:
LC 5??? $ all 5000...GPC-loadcases as in the LC-list in file _csmlf.dat
LC 6??? $ all 6000...AQB creep inner EIGE stresses
LC TYPE 'T'
$ pre superposed container / actions without GPC: (created in _desi.dat MAXIMA run):
LC TYPE 'Y_D ' CST 9998 REF GROS $ CST 9998 = acts on final section (9999 reserved for unbonded tendons)
$ combinations:
COMB MAXD MY TITL 'ULS_elast_maxMY_too' LCST 3100 LC1 G LC2 C LC3 Y_D F3 1.0 LC4 T F4 1.35*0.6
$
COMB GMAX LCST 3112 TITL 'ULS_elast_max'
COMB GMIN LCST 3113 TITL 'ULS_elast_min'
STRE C STYP M0
END
Note that in the approaches sketched above the overall internal forces for the design combination (including temperature!) can only be found in the combinations/loadcases from AQB.
Note also that eigenstresses are not considered if nonlinear effects (e.g. cracking of concrete) appear in a stress calculation with AQB NSTR.